11. Egy kis analízis
/1. Definíció:
Ebben a fejezetben többváltozós vektor értékű
függvényekkel foglalkozunk. Ezek
függvények, ahol
a függvény értelmezési tartománya.
Egy ilyen függvényt
koordinátánként adunk meg:
Ha speciálisan , akkor a függvényt
egyváltozós vektor értékű függvénynek mondjuk.
Ha pedig , akkor valós értékű függvénynek mondjuk.
/2. Konvenció:
Ezt a jelölést az egész fejezetben használjuk: mindig egy
halmazon értelmezett változós értékű
függvényt jelöl, jelöli a koordinátáit.
Ha másképp nem mondjuk, akkor nyílt halmaz.
Ha speciálisan , akkor
helyett gyakran írunk egy inervallumot.
/3. Definíció:
Az függvényt lineáris függvénynek mondjuk,
ha egy méretű mátrix segítségével ilyen alakban
írható:
ahol tetszőleges pontok. Máskép szólva ez azt jelenti,
hogy az koordináta függvények mind ( változós)
lineáris függvények.
Az függvényt
fokú ( változós vektorértékű) polinom-függvénynek
mondjuk, ha a koordináta függvények legfeljebb fokú (
változós) polinomok, és az egyikük ténylegesen fokú.
Függvények közelítése
Ha egy
folytonos függvény, és , akkor definíció szerint
.
Az elkövetkezőkben arra leszünk kíváncsiak, hogy
milyen gyorsan tart a nullához.
Például, ha nagyon kis abszolút értékű szám, akkor
, ezért
az függvény gyorsabban közelít a nullához,
mint az függvény, az pedig mindkettőnél jobban
siet. Ezt teszi precízzé a következő definíció.
/4. Definíció:
Az függvény
első rendben eltűnik a pontban, jelölésben
, ha bármilyen
együtthatóval az
becslés teljesül egy origó körüli kis intervallumon. Természetesen
mennél kisebb -t választunk, annál kisebb intervallumon érvényes
a becslés. Ha pedig adott kitevőre és minden együtthatóra
az
becslés is érvényes az origó környezetében, akkor azt mondjuk,
hogy az függvény -adrendben eltűnik az origóban,
azaz .
/5. Definíció:Közelítő függvények
Legyenek
függvények.
Azt mondjuk, hogy a
függvény
első rendben közelíti
az
függvényt a
pont környezetében, ha a különbségük első rendben eltűnik
a
pontban:
Az
tagot gyakran
hiba-tagnak
hívják, hiszen ő a közelítés hibája.
Ha pedig a hiba-tag
-adrendben is eltűnik:
akkor azt mondjuk, hogy a
fügvény
-ad rendben közelíti az
-et.
Gyakran szeretnénk az függvényt lineáris
függvényekkel közelíteni:
tetszőleges pont környezetében szeretnénk egy ilyen
becslést:
valamilyen -es mátrixszal.
Az a kérdés, melyik esetén lesz a becsés a legpontosabb:
/6. Definíció:Derivált
Az
függvény
differenciálható a
pontban,
ha van olyan lineáris függvény, ami a
pont körül első rendben
közelíti őt. Tehát van egy
méretű mátrix, jelölése
, amelyre
teljesül. Ez a mátrix az
függvény
pontbeli deriváltja, vagy
más néven
differenciálhányadosa.
A
függvényt, amennyiben létezik,
az
deriváltjának hívjuk:
ez az
minden ponthoz egy
méretű mátrixot rendel.
Többféle jelölést is használnak rá:
,
. Ha
differenciálható, és defiváltja folytonos,
akkor
folytonosan differenciálható függvénynek mondjuk.
/I. Feladat:
Van két függvényünk: és , és sikerül őket
elsőrendben megközelíteni az illetve lineáris
függvényekkel. Lásd be, hogy az kompozíciót elsőrendben
közelíti az kompozíció! Pontosítsd az állítást:
melyik pontok környezetében érvényesek a közelítések?
Az előző feladatból azonnal következnek az összetett függvények
deriválására vonatkozó szabály:
/II. Feladat:Összetett függvény deriváltja
Tegyük fel, hogy a függvény differenciálható a
pontban, az függvény pedig differenciálható a
pontban. Lásd be, hogy a kompozíció diferenciálható
a pontban, és derivált mátrixa megegyezik az függvény
-beli és a függvény -beli derivált mátrixának
szorzatával:
/III. Feladat:Inverz függvény deriváltja
Adott az invertálható függvény. Tegyük fel,
hogy a pontban differenciálható. Lásd be, hogy az
inverz függvény is differenciálható az pontban, és a
derivált mátrixa az derivált mátrixának az inverze:
Segítség
Egyváltozós függvények
Legyen egy zárt intervallum.
Egy függvényre úgy gondolunk,
mint egy -vel paraméterezett görbe az dimenziós
térben.
Egy ilyen függvényt koordinátánként tudunk
megadni:
ahol közönséges egyváltozós,
valós értékű függvények.
/IV. Feladat:
Példák egyváltozós függvényekre:
- Add meg egy síkbeli kör paraméteres egyenletét!
- Add meg egy térbeli spirálvonal egyenletét!
/7. Tétel:Görbe érintője
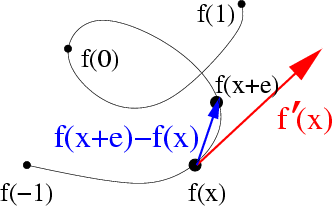
Legyen
egyváltozós függvény, azaz egy
-beli görbe.
A deriváltja - amennyiben létezik - az
képlettel számolhatjuk ki. Amint a rajzon is látható, ez éppen a
görbe érintő vektorát adja, a vektor hossza pedig azt mutatja,
mekkora "sebességgel" halad a
paraméter a görbén. Ha ugyanezt a
görbét másképpen paraméterezzük, akkor ugyanilyen irányú, de más
hosszúságú érintő vektort kapunk.
A határérték koordinátánként is számítható:
/V. Feladat:
Adott az differenciálható görbe,
legyen az abszolút értéke. Ez egy valós szám értékű
folytonos függvény, és differenciálható is azokban a pontokban,
ahol . Lásd be, hogy az ilyen pontokban:
Segítség
/VI. Feladat:
Az differenciálható függvény (görbe)
minden pontban teljesíti az becslést.
Lásd be, hogy ilyenkor
/VII. Feladat:
Az differenciálható függvény (görbe)
minden pontban teljesíti az becslést,
és . Lásd be, hogy ilyenkor minden pontban
SegítségMegoldások
/VIII. Feladat:
Az differenciálható függvény (görbe)
minden pontban teljesíti az
becslést, és .
Lásd be, hogy ilyenkor minden pontban
Segítség
Egyváltozós függvényekkel nagyon gyakran találkozunk. Most csak
arra az esetre koncentrálunk, amikor a függvény valamilyen mennyiség
időbeli változásait írja le - tehát a függvény változója az
idő. Számtalan ilyen példát ismerünk fizikából, kémiából vagy
például a gazdasági életből. Nagyon sokszor ismerünk olyan
törvényszerűségeket, amelyek bizonyos mennyiségek értéke, és
megváltozásuk sebessége közt teremt kapcsolatot. Szemléletünk, és a
tapasztalat azt sugallja, hogy ilyen esetekben e mennyiségek kezdeti
értéke gyakran teljesen meghatározza időbeli fejlődésük menetét.
Ezt a megfigyelést önti formába a következő definíció és
Picard-Lindelöf tétel - ennek a kis analízis-ismertetőnek a
legfontosabb része.
/8. Érdekesség:
Egy meteorológus igyekszik pontos felmérést készít egy
területen arról, hogy melyik pontban milyen irányú és erősségű szél
fúj. A vizsgálat eredményét térképre is rajzolja. Amit végül is
kap, az a mi analízis nyelvünkre lefordítva egy kétváltozós,
vektorértékű függvény - az ilyet vektormezőnek is
hívják. Ha még ennél is alaposabb a meteorológusunk, akkor
különféle magasságokban is elvégzi a felmérést, így a szél térbeli
eloszlásáról kap képet - egy háromváltozós, vektorértékű
függvényt. Egy ilyen felmérésnek sok gyakorlati alkalmazása
lehet. Például, ha nagy mennyiségű mérges gáz kerül a levegőbe,
akkor egy ilyen térkép segítségével megjósolható a gáz
terjedésének iránya, sebessége, és az egész keveredési folyamat
időbeli lefolyása.
A fizikai törvény most roppant egyszerű: a gáz-részecskék spontán
sodródnak a szélben, azaz a sebesség-vektoruk minden pillanatban
megegyezik az aktuális térbeli helyzetükben mért szél
sebesség-vektorával.
Egy részecske mozgását egy egyváltozós
függvénnyel írhatjuk le: minden pillanathoz
hozzárenteljük az akuális helyzetét. A feladat egyszerűnek hangzik:
keressük azt az függvényt, amelyik deriváltja (azaz a
sebesség-vektor) minden pillanatban megegyezik az
pontbeli szélsebességgel.
/9. Definíció:Vektor mező, Differenciál egyenlet
Adott az
dimenziós térben egy
nyílt
halmazán értelmezett vektor-értékű függvény:
. (Figyelem: mindkét tér
!)
Az ilyet
vektormezőnek is mondják.
Az
egyváltozós függvényre vonatkozó
egyenletet
közönséges elsőrendű differenciál egyenletnek
hívjuk. Egy ilyen egyenletet
kezdeti érték feladatnak hívunk, ha
értéke is
adott - geometriai nyelven ez azt jelenti, hogy adott kezdőpontból
induló görbére vadászunk.
Milyen vektormezők esetén tudjuk garantálni a megoldhatóságot?
És a megoldás milyen feltételek mellett lesz egyértelmű?
Sajnos a folytonosság ehhez nem elegendő.
/10. Definíció:Lipshitz tulajdonság
Egy
függvényt
Lipschitz függvénynek hívunk, ha található
olyan
konstans, amelynek segítségével lineárisan becsülhető az
függvény megváltozása: bármely két
pontra teljesül a
becslés. A becslésben szereplő
számot
Lipshitz
konstansnak hívjuk.
Az
függvényt
lokálisan Lipschitz függvénynek
mondjuk, ha az
minden pontjának van olyan környezete, ahová
megszorítva Lipshitz függvényt kapunk.
/IX. Feladat:
Lásd be, hogy az abszolút érték függvény Lipshitz, de nem
differenciálható.
/X. Feladat:
Lásd be, hogy az
függvény folytonos, de nem Lipshitz a pont környezetében.
/XI. Feladat:
Lásd be, hogy egy Lipshitz függvény mindig folytonos.
/XII. Feladat:
Lásd be, hogy egy folytonosan diferenciálható
függvény lokálisan Lipschitz tulajdonságú!
Segítség
/11. Tétel:Picard-Lindelöf tétel
Legyen
egy, az
nyílt
halmazon értelmezett lokálisan Lipschitz vektormező.
Tegyük fel, hogy
sehol sem veszi fel a 0 értéket.
Akkor tetszőleges
kezdőponból az
kezdeti érték feladatnak a
pont van egyetlen megoldása a
pont egy kis környezetében. Azaz: van egy kis origó körüli
intervallum, és egy azon értelmezett
megoldás függvény,
továbbá bármely két megoldás megegyezik a
egy (esetleg még
szűkebb) környezetében.
A tétel
"szokványos" bizonyítását
most nem ismétlem, helyette lássunk egy másikat.
A most következő becslés a bizonyítás kulcs-lépése.
Azt mondja ki, hogy ha két görbe közelítőleg
( hibával) megoldja a differenciál egyenletet, és a két
görbe egymáshoz közeli pontokból indult, akkor ugyan távolodhatnak
egymástól, de nem akármilyen gyorsan. Az a lényeg, hogy a becslés
-től független, és minden tag kicsi lesz,
ha az intervallumot kellően rövidre választjuk:
/XIII. Feladat:
Adott az Lipschitz függvény
Lipschitz konstanssal,
és az görbék minden pontban kielégítik az
becslést. Lásd be, hogy ha , akkor
bármely pontban:
Segítség
A tétel ezek után úgy bizonyítható, hogy megpróbálunk olyan
görbéket készíteni, akik egyre nagyobb pontosságal oldják meg
az egyenletet. Például így:
Először az halmazt kicseréljük a kezdőponk olyan környezetére,
amelyikem már Lipschitz tulajdonságú.
A intervallumot felosztjuk
egyenlő részre, és az görbe töröttvonal lesz,
balról jobbra, szakaszonként definiáljuk.
Amikor az -edik szakaszhoz érünk, a
kezdőpont megegyezik az előző szakasz végpontjával, tehát
már ismert.
Ebből a kezdőpontból a görbe egyenes vonalon
egyenletes sebességgel haladjon tovább az egész -edik szakaszon,
úgy, hogy a deriváltja éppen legyen.
Képlettel is megadhatjuk:
Könnyű belátni, hogy ha elég kicsi, akkor a töröttvonal nem
hagyja el az tartományt, és az összes is egy közös
korlát alatt marad. Ez a töröttvonal még nem teljesen jó:
a töréspontokban nem differenciálható. Vagy lekerekítjük a sarkokat,
vagy éppenséggel a
/XIII. Feladatot
is kiterjeszthetjük töröttvonalakra.
Mivel minden szakaszunk hossza , azért az -edik
szakaszon így becsülhetünk:
Ha -et növeljük, akkor ez akármilyen kicsivé
tehető. Alkalmazzuk a
/XIII. Feladatot az és
görbékre!
Kiderül, hogy ha és nagyon nagyok, akkor a két görbe nagyon
közel van egymáshoz. Ezért létezik egy határérték görbe - és az már
valóban megoldása az egyenletnek.
A /XIII. Feladat másik fontos
alkalmazása, hogy a megoldás-görbe folytonosan függ a kezdőponttól:
ha folytonosan változtatjuk a kezdőpontot, akkor az (egyértelmű)
megoldás görbe is folytonosan változik. Ezt érdemes tételként is
kimondani:
/12. Tétel:Vektormező folyama
Adott az
lokálisan Lipschitz vektormező, és egy
korlátos zárt halmaz. Ekkor elég kis
választása mellett létezik
változós
Lipschitz függvény, amelyet bármely
pontra megszorítva az
függvény az
kezdeti érték feladat megoldása. Mivel ez a megoldás egyértelmű,
azért csak egyetlen ilyen
van. Ez az
vektormező folyama.
/13. Érdekesség:
A korábbi meteorológiai példában egy gázfelhő részecskéinek a
mozgását akartuk követni. A vektormező (a szél) folyama egyszerre
adja meg az összes részecske mozgását, valójában erre is voltunk
kíváncsiak. És innen ered az elnevezés is: folyadékokban, gázokban
az áramlási sebesség vektor-mezőjének folyama nem más, mint
a részecskék mozgása - tehát amit a köznapi életben is folyamnak
hívnánk.
/14. Megjegyzés:
Egy vektormező folyama mindig olyan "szép",
mint a vektormező. Mindig Lipshitz függvény, de ha a vektormező
például differenciálható, és a deriváltja is Lipschitz, akkor a
folyam is ilyen tulajdonságú.
Ez azon múlik, hogy a folyam deriváltjaira is könnyű felírni
differenciál egyenletet.
/15. Megjegyzés:
Az
vektormezőtől is folytonosan függ a megoldás. Ez is a
/XIII. Feladat következménye.
Most lássunk néhány következményt.
Ezekhez nem kell tudni a bizonyítást - elegendő hozzájuk a
Picard-Lindelöf tétel
ismerete:
/XIV. Feladat:
Lásd be, hogy a
Picard-Lindelöf
tételben
két megoldás nem csak egy kis környezetben egyezik meg, hanem az
értelmezési tartományuk (azaz a két intervallum) teljes közös
részén.
/XV. Feladat:
Lásd be, hogy a
Picard-Lindelöf tétel
feltételei mellett a kezdeti érték feladatnak van (egyértelmű)
maximális megoldása:
azaz van egy tovább már nem bővíthető intervallum, és
egy megoldásfüggvény.
/XVI. Feladat:
Az előző feladatban maximális megoldást készítettél. Most lásd be,
hogy csak kétféle oka lehet annak, hogy a maximális megoldás nem
folytatható a b ponton túl: Vagy a -beli határértéke az
tartomány határán van, vagy .
Többváltozós függvények
Ebben a jegyzetben fontos lesz a dimenzió fogalma. Algebrában,
analízisben, topológiában számtalan változatban definiálnak
dimenziót, de "szép" alakzatokra ezek ugyanazt a számot adják. Mi
most megelégszünk egy viszonylag egyszerű dimenzió fogalommal.
Az azon részhalmazait, amelyeknek minden pontban van
"érintője", és az mindenütt egy -dimenziós altér, -dimenziós
részsokaságoknak nevezzük.
A részsokaságokat kétféleképpen is meg lehet adni: paraméteres
egyenlettel, vagy egyenletrendszer megoldás-halmazaként. A két
megadási mód kétféle definícióhoz vezet - szerencsére a két
definíció ekvivalens.
/16. Definíció:Részsokaság (egyenlettel)
Most
.
Egy
részhalmazt
részsokaságnak
hívunk, ha megegyezik egy
folytonosan
differenciálható függvény valamelyik szintfelületével
(például a zérushelyével), ahol
egy nyílt környezet, és az
deriváltja mindenütt
rangú (azaz szürjektív). Az így
kapott sokaság
dimenziója
.
A
részsokaság érintőtere egy
pontban
egy
dimenziós affin altér
-ben:
úgy kapjuk meg, hogy a
derivált magját eltoljuk a
pontba.
/17. Definíció:Részsokaság (paraméterezve)
Most
.
Egy
részhalmazt
-dimenziós
részsokaságnak nevezünk, ha minden
pontjának
van egy
nyílt környezete, amelybe
eső részét a következő módon lehet megadni:
Van egy
nyílt halmaz, és egy
folytonosan differenciálható
függvény, amelynek deriváltja minden pontban
rangú (azaz
injektív), és amelynek képe éppen
.
A sokaság
pontbeli érintő tere egy
dimenziós affin altér
-ben, így kaphatjuk: a
-beli derivált
képterét eltoljuk a
pontba.
A két definíció ekvivalens. Ezt órán beláttuk, de most csak
annyit írok, hogy az Inverz Függvény Tételből következett.
/XVII. Feladat:
Lásd be, hogy minden véges részhalmaza 0 dimenziós
részsokaság - mindkét definíció szerint! Sőt, minden diszkrét részhalmaz
0 dimenziós részsokaság.
/XVIII. Feladat: Lásd be, hogy -dimenziós affin alterei
dimenziós részsokaságok.
/XIX. Feladat:
Lásd be, hogy egy gömbfelület a térben 2-dimenziós részsokaság -
mindkét definíció szerint! Lásd be, hogy az érintő tere mindkét
definíció szerint megegyezik a hagyományos érintő síkkal!
/XX. Feladat:
Lásd be, hogy nyílt részhalmaza -dimenziós
részsokaság - mindkét definíció szerint! Mi az érintő tere?
/XXI. Feladat:
Lásd be, hogy egy kocka felszülete nem részsokaság - egyik
definíció szerint sem!
/XXII. Feladat:
Mikor lesz két síkbeli egyenes uniója részsokaság?
Segítség
/XXIII. Feladat:
Ugyanazt a részsokaságot sokféle függvény zérushelyeként
megkaphatjuk.
Lásdbe, hogy a két definíció ekvivalenciájából következik, hogy az
érintő tér, és a dimenzió nem függ az választásától!
A következő tétel ezen a ponton néhéz, ezért nem is próbáljuk
bizonyítani:
/18. Tétel:
minden zárt részcsoportja részsokaság
-ben.
A /III. Feladatban láttuk,
hogy egy invertálható függvény derivált mátrixa is invertálható.
Érdemes elgondolkodni rajta, vajon igaz-e fordítva? A válasz -
teljes általánosságban - nemleges. De a derivált folytonosságát is
feltételezve már pozitív eredményhez jutunk:
/19. Tétel:Inverz Függvény Tétel
Adott az
nyílt halmaz,és az
folytonosan differenciálható
függvény. (Figyelem: mindkét dimenzió
!) Tegyük fel, hogy a
pontban a
derivált invertálható. Ekkor az
függvény megszorítása a
pont egy elég kis környezetére
invertálható, az inverz függvény is differenciálható, és deriváltja
az
deriváltjának inverze:
Most nem bizonyítjuk, akit érdekel, megnézheti
például itt.
Csoportok
A csoportelméletben nagyon fontos szerepet kapnak a Lie
csoportok. Ezek olyan csoportok, amelyek egyúttal sokaságok is, és a
csoport-műveletek differenciálhatók. A precíz definíciót most
elhagyjuk - mi csak olyan Lie csoportokkal foglalkozunk, amelyek
zárt részcoportjai:
/20. Definíció:Mátrix Lie csoport
Egy
részcsoportot, amelyik egyben
részsokaság is,
mátrix Lie csoportnak mondunk.
/21. Tétel:Zárt részcsoportok
Egy
mátrix Lie csoport mindig zárt
részcsoport, és fordítva: a zárt részcsoportok mind részsokaságok,
tehát mátrix Lie csoportok.
/22. Megjegyzés:
Nem minden Lie csoport mátrix csoport - de nehéz ellenpéldát
mutatni. Az azonban igaz, hogy minden összefüggő Lie csoport
"közel" van egy mátrix Lie csoporthoz: van egy diszkrét
normálosztója, ami szerint vett faktorcsoport mátrix csoport.
 Legyen egyváltozós függvény, azaz egy
-beli görbe.
A deriváltja - amennyiben létezik - az
képlettel számolhatjuk ki. Amint a rajzon is látható, ez éppen a
görbe érintő vektorát adja, a vektor hossza pedig azt mutatja,
mekkora "sebességgel" halad a paraméter a görbén. Ha ugyanezt a
görbét másképpen paraméterezzük, akkor ugyanilyen irányú, de más
hosszúságú érintő vektort kapunk.
A határérték koordinátánként is számítható:
Legyen egyváltozós függvény, azaz egy
-beli görbe.
A deriváltja - amennyiben létezik - az
képlettel számolhatjuk ki. Amint a rajzon is látható, ez éppen a
görbe érintő vektorát adja, a vektor hossza pedig azt mutatja,
mekkora "sebességgel" halad a paraméter a görbén. Ha ugyanezt a
görbét másképpen paraméterezzük, akkor ugyanilyen irányú, de más
hosszúságú érintő vektort kapunk.
A határérték koordinátánként is számítható: