2. A kör egybevágóságai: O(2), SO(2)

Megoldás: Az egyetlen egybeesés: az identitás egyúttal $0$ fokos elforgatás is. A forgatások irányítás tartó transzformációk, a tükrözések pedig megfordítják a kör irányítását -- ezért senki sem lehet egyszerre tükrözés és elforgatás is.

Megoldás: Az egybevágóság a kör középpontját, és a $P$--vel átellenes $Q$ pontot is helyben hagyja. Ezért a két $\mathrm{PQ}$ félkör ívet vagy saját magukba viszi, vagy felcseréli őket. Ráadásul, egy íven belül minden pontot egyértelműen meghatároz a $P$--től mért távolsága, ezért csak egyetlen olyan egbevágóság van, amelyik a két ívet magába viszi, és csupán egyetlen olyan egybevágóság van, amelyik felcseréli őket.

Megoldás: Legyen $\varphi$ egy egybevágóság. Válasszunk egy tetszőleges $P\in K$ pontot a körön, $\varphi \left(P\right)$ jelöli a transzformáltját. Legyen $\psi$ az a tükrözés, amelyik a $P$ pontot felcseréli a $\varphi \left(P\right)$ képével (tehát a $\mathrm{PO}\varphi \left(P\right)$ szög felezőjére tükrözünk). Ekkor az $\rho =\varphi \psi$ kompozíció egy olyan egybevágóság, amelyik a $P$ pontot helyben hagyja. Láttuk az előző feladatban, hogy ez vagy az identitás, vagy egy tükrözés. Tehát $\varphi =\rho \psi$ vagy megegyezik a $\psi$ tükrözéssel, vagy pedig két tükrözés kompozíciója -- azaz egy forgatás.

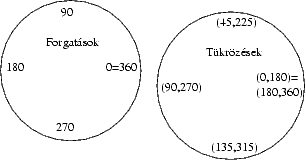
Megoldás: A rajznak két komponense lesz: a forgatások, és a tükrözések. A forgatásokat a szögükjellemzi, legkényelmesebben egy körvonalra rajzolhatjuk fel az összes lehetséges szöget ($0^{\circ }$-tól ${360}^{\circ }$-ig). A tükrözéseket pedig a fixpontjukkal jellemezhetjük, tehát egy átellenes pontpárral a körön -- ezeket egy másik körvonalra rajzolhatjuk, és itt minden pontot két (átellenes) szöggel is megcímkézünk. A rajz természetesen nem egyértelmű, de nem is lehet akármilyen. Ha például a tükrözéseket a $[0^{\circ },{180}^{\circ })$ intervallummal akarnánk ábrázolni, akkor a folytonosság sérülne: az intervallum két végének a valóságban nagyon közeli tükrözéseknek felel meg.