33.1. Definíció (Poincaré-sor). Legyen V = ⊕ n=0∞V n egy olyan fokszámozott vektortér egy tetszőleges test felett, melynek minden homogén komponense véges dimenziós. Az alábbi hatványsort a V Poincaré-sorának nevezzük:
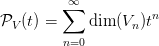
33.1. Definíció (Poincaré-sor). Legyen V = ⊕ n=0∞V n egy olyan fokszámozott vektortér egy tetszőleges test felett, melynek minden homogén komponense véges dimenziós. Az alábbi hatványsort a V Poincaré-sorának nevezzük:
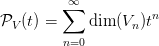
33.2. Megjegyzés. Ha A = ⊕
n=0∞A
n egy végesen generált
fokszámozott gyűrű, akkor A ⊗ ℚ egy olyan fokszámozott algebra a
racionális szám-test felett, melynek minden homogén komponense véges
dimenziós, ezért beszélhetünk a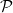 
A⊗ℚ(t) Poincaré-sorról. A homogén
generátor-rendszer mérete szerinti indukcióval bizonyítható, hogy ebben
az esetben a Poincaré-sor összege egy racionális törtfüggvény.
