32. Grassmann sokaság
32.1. Definíció (Grassmann sokaság).
Legyenek 0 < k < n egész-számok, V egy n-dimenziós valós
(illetve komplex) vektortér. A Grassmann-sokaság a V -beli k-dimenziós
lineáris altereket paraméterezi, szokásos jelölések: Gr(k,V ), Gk(V ),
Gr(k,n). A Grassmann-sokaság pontjai tehát a k-dimenziós alterek
V -ben, térképeket pedig így kapunk:
Válasszunk egy V = X0 ⊕ F direkt felbontást, ahol dim(X0) = k
és dim(F) = n − k. Jelölje U ⊂ GR(n,V ) az olyan X < V
k-dimenziós alterek halmazát, melyekre X ∩ F = {0}. Minden ilyen
alterek egy X0 → F homomorfizmus grafikonja, így U-t azonosítottuk a
Hom(X0,F) vektortérrel. Ez egy térkép az U ⊂ Gr(n,V ) részhalmazon.
Tekintsük az összes lehetséges V = X0 ⊕ F felbontást, így az
egész Grassmann sokaságot lefedjük térképekkel, tehát Gr(k,V ) egy
differenciálható sokaság (illetve komplex sokaság).
32.2. Feladat. Lásd be, hogy az U halmaz csak az F altértől függ, az
X0-tól független! Lásd be, hogy a térképek lefedik az egész Grassmann
sokaságot! Lásd be, hogy a térképek közötti koordináta-transzformációk
differenciálhatók (sőt, polinomok)!
32.5. Definíció (Univerzális nyaláb). Tekintsük a Gr(k, ℝ∞) × ℝ∞
triviális vektor-nyalábban az olyan (V,x) párok részhalmazát (emélkezz:
V altér, x pedig vektor ℝ∞-ben), melyekre az x vektror benne van a V
altérben! Ez a részhalmaz egy k-rangú vektor-nyaláb, amit univerzális
nyalábnak hívunk, és γk-val jelölünk.
Az univerzális nyaláb elnevezést az alábbi tétel indokolja:
32.6. Tétel. Legyen X egy CW-komplexus! Tetszőleges f :
X → Gr(k, ℝ∞) folytonos leképezéshez redeljük hozzá az f∗γ
k
vektor-nyalábot. Ez egy bijekciót ad az X feletti k-rangú vektor-nyalábok
izomorfia-osztályai, és az X → Gr(k, ℝ∞) folytonos leképezések
homotópia-osztályai között.
32.7. Feladat. Fogalmazd meg a 32.4. Definíció és a 32.6. Tétel
komplex vektornyalábokra vonatkozó variánsát!
32.8. Definíció (Schubert-cellák). Legyen σ = (σ1,σ2,…,σk) egy
olyan egészszámokból álló sorozat, melyre 1 ≤ σ1 < σ2 <  < σk.
Használjuk a 32.3. Konstrukció jelölését. A σ Schubert-szimbólumhoz
tartozó (valós) Schubert-cella, eσ ⊂ Gr(k, ℝ∞), az olyan X < ℝ∞
k-dimenziós alterek halmaza, melyekre
< σk.
Használjuk a 32.3. Konstrukció jelölését. A σ Schubert-szimbólumhoz
tartozó (valós) Schubert-cella, eσ ⊂ Gr(k, ℝ∞), az olyan X < ℝ∞
k-dimenziós alterek halmaza, melyekre
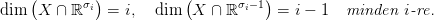 A σ-hoz tartozó
A σ-hoz tartozó komplex Schubert-cella
, eσℂ ⊆ Gr(k, ℂ∞), az olyan
X < ℂ∞ komplex alterek halmaza, melyekre
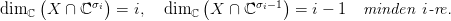
32.9. Tétel. A eσℂ ⊂ Gr(k, ℂ∞) részhalmaz egy cella, dimenziója
![[ ]
dim(e ) = 2 (σ − 1) + (σ − 2) + ⋅⋅⋅ + (σ − k) .
σ 1 2 k](algebrai-topologia607x.png) A komplex Schubert-cellák páronként diszjunktak, és a Gr(k, ℂ∞) Grassmann-sokaság
CW-felbontását adják. A Gr(k, ℂn) Grassmann-sokaság pedig egy CW-rész-komplexus:
azon Schubert-cellákból áll, melyekre σk ≤ n.
A komplex Schubert-cellák páronként diszjunktak, és a Gr(k, ℂ∞) Grassmann-sokaság
CW-felbontását adják. A Gr(k, ℂn) Grassmann-sokaság pedig egy CW-rész-komplexus:
azon Schubert-cellákból áll, melyekre σk ≤ n.
Bizonyítás. Be kell látni, hogy eσ egy ...-dimenziójú cella, és a pereme
benne van a kisebb cellák uniójában. Ezért tényleg CW-komplexus.
Egy X ∈ eσ altér pontosan akkor van benne ℝn-ben, ha σ
k ≤ n.
Minden ℝn-beli k-dimenziós altér benne van pontosan egy e
σ-ban.
Ezért a CW-komplexus kitölti az egész végtelen Grassmann-sokaságot,
és Gr(n, ℝn) éppen a megadott CW-rész-komplexus. □
32.10. Tétel. Az eσ ⊂ Gr(k, ℝ∞) részhalmaz egy cella, dimenziója
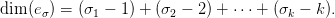 A Schubert-cellák páronként diszjunktak, és a Gr(k, ℝ∞) Grassmann-sokaság
CW-felbontását adják. A Gr(k, ℝn) Grassmann-sokaság pedig egy CW-rész-komplexus:
azokból a Schubert-cellákból áll, melyekre σk ≤ n.
A Schubert-cellák páronként diszjunktak, és a Gr(k, ℝ∞) Grassmann-sokaság
CW-felbontását adják. A Gr(k, ℝn) Grassmann-sokaság pedig egy CW-rész-komplexus:
azokból a Schubert-cellákból áll, melyekre σk ≤ n.
32.11. Tétel. A komplex végtelen Grassmann
sokaság kohomológia-gyűrűje egy polinom-gyűrű k generátorral, melyek
fokai rendere 2, 4, 6,…, 2k. A 2i-fokú generátort i-edik Chern-osztálynak
hívjuk, ci-vel jelöljük.
![( )
H ∗ Gr (k,ℂ ∞);ℤ = ℤ [c ,c ,...,c ], deg(c ) = 2i
1 2 k i](algebrai-topologia609x.png)
Bizonyítás. Tekintsük
a Gr(k, ℂ∞) Grassmann-sokaság 32.8. Definícióban megkonstruált
CW-felbontását. Ebben minden cella
páros-dimenziós, tehát a H2m Gr(k, ℂ∞); ℤ
Gr(k, ℂ∞); ℤ kohomológia-csoportok
mind szabad Abel-csoportok, rangjuk megegyezik az 2m-dimenziós
cellák számával, tehát az olyan σ = (σ1,σ2,…,σk) egész-szám sorozatok
számával, melyekre
kohomológia-csoportok
mind szabad Abel-csoportok, rangjuk megegyezik az 2m-dimenziós
cellák számával, tehát az olyan σ = (σ1,σ2,…,σk) egész-szám sorozatok
számával, melyekre
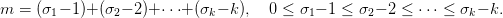
Másrészt, tekintsük az
![A = ℤ[c ,c ,...,c ], deg(c) = 2i
1 2 k i](algebrai-topologia613x.png)
polinom-gyűrűt. Definíció szerint a
c1r1c
2r2 c
krk
c
krk monom foka
r
1 +
2r2 +  + krk
+ krk, tehát az
A gyűrű
2m-fokú homogén komponensének
rangja megeryezik az olyan
r = (r1,r2,…,rk) sorozatok számával, melyekre
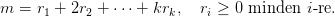
Minden egyes ilyen
r sorozathoz rendejük hozzá azt a
σ sorozatot,
amelyre
σ1 − 1 = rk,
σ2 − 2 = rk + rk−1, és általában
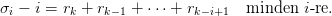
Ez a sorozat kielégíti a
σ-re szabott feltételeket, és könnyen visszakapható
belőle az eredeti
r-sorozat. Tehát minden
m-re pontosan ugyanannyi
r
sorozat van, mint ahány
σ sorozat. Ezzel beláttuk, hogy a
H2m Gr(k, ℂ∞); ℤ
Gr(k, ℂ∞); ℤ
Abel-csoport izomorf az
A gyűrű
2m-fokú homogén komponensével,
tehat a kohomológia-gyűrű, mint fokszámozott Abel-csoport, izomorf
A-val.
A gyűrű-struktúrát később, a zászló-sokaságok segítségével
határozzuk meg. □
32.12. Definíció (Zászló sokaság).
ℂn-beli k-dimenziós teljes zászlónak hívjuk az olyan (L
1,L2,…,Lk)
k-asok halmazát, ahol Li ≤ ℂn páronként ortogonális egy-dimenziós
komplex alterek. Jelölje  (k, ℂn) az összes ℂn-beli k-dimenziós zászló
halmazát — ez könnyen elllátható topológiával, sőt, differenciálható
sokasággá tehető, ezért zászló-sokaságnak hívjuk. A 32.3. Konstrukció
természetes beágyazásokat indukál, ezért definiálhatjuk a végtelen
zászló-sokaságot is:
(k, ℂn) az összes ℂn-beli k-dimenziós zászló
halmazát — ez könnyen elllátható topológiával, sőt, differenciálható
sokasággá tehető, ezért zászló-sokaságnak hívjuk. A 32.3. Konstrukció
természetes beágyazásokat indukál, ezért definiálhatjuk a végtelen
zászló-sokaságot is:
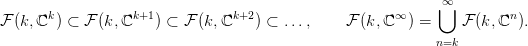
32.14. Megjegyzés. Sokan
a 32.13. Feladatban leírt módon definiálják a zászló-sokaságot. Ennek
a módszernek megvan az az előnye, hogy nem használ merőlegességet,
így tetszőleges testre is általánosítható.
32.15. Feladat. Rögzítsünk egy Hk < Hk−1 <  < H1 < ℂn
altér-láncot, ahol dim(Hi) = n − i minden i-re! Azt mondjuk, hogy
egy (L1,…,Lk) zászló transzverzális a {Hi} altér-láncra, ha Li ⁄⊂ Hi
minden i-re. Mutass egy bijekciót a {Hi} altér-láncra transzverzális
zászlók és az ⊕i=1kH
i vektortér elemei között! Lásd be, hogy ezen a
módon
< H1 < ℂn
altér-láncot, ahol dim(Hi) = n − i minden i-re! Azt mondjuk, hogy
egy (L1,…,Lk) zászló transzverzális a {Hi} altér-láncra, ha Li ⁄⊂ Hi
minden i-re. Mutass egy bijekciót a {Hi} altér-láncra transzverzális
zászlók és az ⊕i=1kH
i vektortér elemei között! Lásd be, hogy ezen a
módon  (k, ℂn) sokasággá tehető! Mennyi a dimenziója?
(k, ℂn) sokasággá tehető! Mennyi a dimenziója?
Ötlet. Ahhoz, hogy sokaságot kapjunk, fel
kell írnunk a koordináta-transzformációt két különböző altér-lánchoz
tartozó térkép között. □
32.16. Feladat. Minden i = 1, 2,…,k értékre tekintsük azt a ϕi :
 (k, ℂ∞) → ℂℙ∞ leképezést, ami az (L
1,…,Lk) zászlóhoz az Li egyenest
rendeli! (A projektív tér az origón átmenő egyenesek tere.) Bizonyítsd
be, hogy ϕi folytonos! Mutasd meg, hogy ϕi egy
(k, ℂ∞) → ℂℙ∞ leképezést, ami az (L
1,…,Lk) zászlóhoz az Li egyenest
rendeli! (A projektív tér az origón átmenő egyenesek tere.) Bizonyítsd
be, hogy ϕi folytonos! Mutasd meg, hogy ϕi egy  (k − 1, ℂ∞)-nyaláb
(lásd a 12.2. Definíciót)!
(k − 1, ℂ∞)-nyaláb
(lásd a 12.2. Definíciót)!
32.17. Feladat. Tekintsük
i = 1, 2,…,k-ra a 32.16. Feladat ϕi :  (k, ℂ∞) → ℂℙ∞ leképezéseit!
A végtelen projektív tér kohomológia-gyűrűje a ℤ[c1] polinom-gyűrű
(lásd a 31.1. Példát), vezessük be az xi = ϕi∗c
1 jelölést! (Ezek
mind második kohomológia-osztályok.) Lásd be, hogy a zászló-sokaság
kohomológia-gyűrűje
(k, ℂ∞) → ℂℙ∞ leképezéseit!
A végtelen projektív tér kohomológia-gyűrűje a ℤ[c1] polinom-gyűrű
(lásd a 31.1. Példát), vezessük be az xi = ϕi∗c
1 jelölést! (Ezek
mind második kohomológia-osztályok.) Lásd be, hogy a zászló-sokaság
kohomológia-gyűrűje
![( )
H ∗ F (k,ℂ ∞ );ℤ ∼= ℤ [x1,x2,...,xk], deg (xi) = 2minden i-re!](algebrai-topologia623x.png)
Ötlet.  (1, ℂ∞) = ℂℙ1, tehát k = 1-re igaz az állítás.
(Lásd a 31.1. Példát!) Az általános esetet k-szerinti indukcióval
bizonyíthatjuk. A 32.16. Feladat szerint ϕk egy
(1, ℂ∞) = ℂℙ1, tehát k = 1-re igaz az állítás.
(Lásd a 31.1. Példát!) Az általános esetet k-szerinti indukcióval
bizonyíthatjuk. A 32.16. Feladat szerint ϕk egy  (k−1, ℂ∞)-nyaláb. A
rost tehát szintén zászló-sokaság, így annak is definiálhatjuk a „saját
xi kohomológia-osztályait” (i < k esetén) — a félreértés elkerülése
végett ezeket xi′-vel jelöljük. Mutasd meg, hogy i = 1, 2,…,k − 1-re,
ha az xi kohomológia-osztályt egy rostra megszorítjuk, akkor az xi′
osztályát kapjuk!
(k−1, ℂ∞)-nyaláb. A
rost tehát szintén zászló-sokaság, így annak is definiálhatjuk a „saját
xi kohomológia-osztályait” (i < k esetén) — a félreértés elkerülése
végett ezeket xi′-vel jelöljük. Mutasd meg, hogy i = 1, 2,…,k − 1-re,
ha az xi kohomológia-osztályt egy rostra megszorítjuk, akkor az xi′
osztályát kapjuk!
Az indukciós feltétel szerint tehát a kohomológia-gyűrűben az
x1,x2,…,xk−1 osztályok által generált részgyűrű egy polinom-gyűrű.
A polinom-gyűrű szabad Abel-csoport, tehát alkalmazhatjuk a ϕk
nyalábra a Leray-Hirsch tételt (lásd a 28.1. Tételt). Ezért  (k, ℂ∞)
kohomológia-gyűrűje egy szabad ℤ[xk]-modulus, melynek bázisát az
x1,x2,…,xk−1 változókból épített monomok alkotják. Ebből már
következik az állítás. □
(k, ℂ∞)
kohomológia-gyűrűje egy szabad ℤ[xk]-modulus, melynek bázisát az
x1,x2,…,xk−1 változókból épített monomok alkotják. Ebből már
következik az állítás. □
32.18. Feladat. Mutasd meg, hogy a  (k, ℂn) zászló-sokaság
kohomológia-gyűrűje szabad Abel-csoport!
(k, ℂn) zászló-sokaság
kohomológia-gyűrűje szabad Abel-csoport!
Ötlet. A 32.16. Feladat mintájára konstruálj egy  (k − 1, ℂn−1) →
(k − 1, ℂn−1) →
 (k, ℂn) → ℂℙn−1 nyalábot! Alkalmazd a Leray-Hirsh tételt (lásd a
28.1. Tételt), k szerinti teljes indukcióval bizonyítsd az állítást! □
(k, ℂn) → ℂℙn−1 nyalábot! Alkalmazd a Leray-Hirsh tételt (lásd a
28.1. Tételt), k szerinti teljes indukcióval bizonyítsd az állítást! □
Alternatív ötlet. A Schubert-cellák mintájára itt is konstruálhatunk
CW-felbontást csupa páros-dimenziós cellával. □
32.20. Feladat. Tekintsük a 32.19. Feladatbeli ϕ nyalábot! Bizonyítsd
be, hogy a
![( ) ( )
ϕ∗ : H ∗ Gr (k,ℂ ∞ );ℤ → H ∗ F (k,ℂ ∞ );ℤ ∼= ℤ [x1,...,xk]](algebrai-topologia625x.png) homomorfizmus injektív, és a képe éppen a szimmetrikus polinomok
rész-gyűrűje! Tehát a Grasmann-sokaság kohomológia-gyűrűje valóban a
32.11. Tételben megadott polinom-gyűrű.
homomorfizmus injektív, és a képe éppen a szimmetrikus polinomok
rész-gyűrűje! Tehát a Grasmann-sokaság kohomológia-gyűrűje valóban a
32.11. Tételben megadott polinom-gyűrű.
Ötlet. Permutáld az egyeneseket a  (k, ℂ∞)-beli zászlókban! Így hat
az Sk szimmetrikus csoport a zászló-sokaságon. Lásd be, hogy az Sk
hatás az xi kohomo-lógia-generátorokat is permutálja! Lásd be, hogy
a ψ leképezés Sk-invariáns! Ezért ψ∗ képe szimmetrikus polinomokból
áll.
(k, ℂ∞)-beli zászlókban! Így hat
az Sk szimmetrikus csoport a zászló-sokaságon. Lásd be, hogy az Sk
hatás az xi kohomo-lógia-generátorokat is permutálja! Lásd be, hogy
a ψ leképezés Sk-invariáns! Ezért ψ∗ képe szimmetrikus polinomokból
áll.
Alkalmazd a Leray-Hirsh tételt a ϕ nyalábra! Abból következik,
hogy ψ∗ injektív, és a képe direkt összeadandó. A 32.11. Tétel
bizonyításában már láttuk, hogy Hn Gr(k, ℂ∞); ℤ
Gr(k, ℂ∞); ℤ ugyanakkora
rangú, mint a homogén n-fokú szimmetrikus polinomok csoportja.
ugyanakkora
rangú, mint a homogén n-fokú szimmetrikus polinomok csoportja.
Lásd be, hogy egy G véges rangú szabad Abel-csoportban
minden valódi direkt összeadandónak kisebb a rangja, mint G-nek.
Ebből következik, hogy ψ∗ képe egyenlő a szimmetrikus polinomok
gyűrűjével. □
32.21. Tétel. A valós végtelen Grassmann sokaság ℤ2-együtthatós
kohomológia-gyűrűje egy polinom-gyűrű
k generátorral, melyek fokai rendere 1, 2, 3,…,k. Az i-fokú generátort
i-edik Stiefel-Whitney-osztálynak hívjuk, wi-vel jelöljük.
![( )
H ∗ Gr(k,ℝ ∞ );ℤ2 = ℤ2[w1,w2, ...,wk], deg(wi ) = i](algebrai-topologia628x.png)
Bizonyítás. A 32.10. Tétel ad egy CW-felbontást. Be kell látni,
hogy egy m-dimenziós Schubert-cella pereme minden (m −
1)-dimenziós cellát vagy kétszer fed le, vagy nullaszor. Ezért a
CW-lánc-komplexusban minden differenciál nulla. A bizonyítás többi
rész ugyanaz, mint a komplex Grassmann-sokaság esetében. □
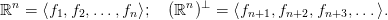
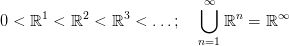
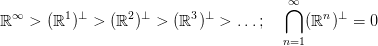
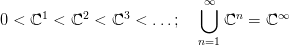
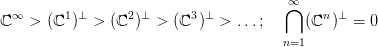
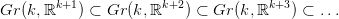
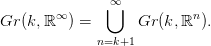
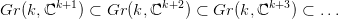
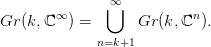

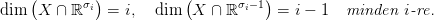
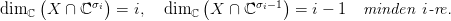
![[ ]
dim(e ) = 2 (σ − 1) + (σ − 2) + ⋅⋅⋅ + (σ − k) .
σ 1 2 k](algebrai-topologia607x.png)
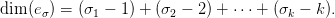
![( )
H ∗ Gr (k,ℂ ∞);ℤ = ℤ [c ,c ,...,c ], deg(c ) = 2i
1 2 k i](algebrai-topologia609x.png)


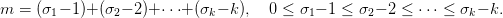
![A = ℤ[c ,c ,...,c ], deg(c) = 2i
1 2 k i](algebrai-topologia613x.png)


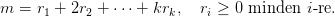
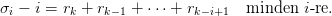



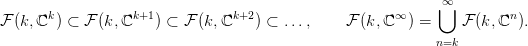


![( )
H ∗ F (k,ℂ ∞ );ℤ ∼= ℤ [x1,x2,...,xk], deg (xi) = 2minden i-re!](algebrai-topologia623x.png)

![( ) ( )
ϕ∗ : H ∗ Gr (k,ℂ ∞ );ℤ → H ∗ F (k,ℂ ∞ );ℤ ∼= ℤ [x1,...,xk]](algebrai-topologia625x.png)


![( )
H ∗ Gr(k,ℝ ∞ );ℤ2 = ℤ2[w1,w2, ...,wk], deg(wi ) = i](algebrai-topologia628x.png)