12. Lokális rendszerek, lapos nyalábok
12.1. Definíció. Legyenek X, Y , Z topológikus terek, f : Y → X
és g : Z → X folytonos függvények. Azt mondjuk, hogy f és g izomorf
X felett, ha van olyan h : Y → Z homeomorfizmus, amelyet g-vel
komponálva éppen f-hez jutunk. Ilyenkor használjuk még a következő
kifejezéseket is: h egy relatív homeomorfizmus (X felett), Y és Y
relatívan, vagy rostonként homeomorfak (X felett).
12.2. Definíció (nyaláb). Legyenek X, Y és F topológikus terek,
f : Y → X egy folytonos függvény. Azt mondjuk, hogy f lokálisan
triviális, és F a rostja, ha X minden pontjának van olyan U környezete,
amelyben az F U : f−1(U) → U megszorítás U felett izomorf az
F × U → U projekcióval. Ezeket az U feletti izomorfizmusokat lokális
trivializációknak hívjuk. Ilyen esetben azt mondjuk, hogy f : Y → X
egy F-nyaláb (angolul: F-bundle), vagy másképpen, F → Y
U : f−1(U) → U megszorítás U felett izomorf az
F × U → U projekcióval. Ezeket az U feletti izomorfizmusokat lokális
trivializációknak hívjuk. Ilyen esetben azt mondjuk, hogy f : Y → X
egy F-nyaláb (angolul: F-bundle), vagy másképpen, F → Y 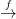 X egy
nyaláb , vagy fibrált nyaláb (angolul: fibre boundle).
X egy
nyaláb , vagy fibrált nyaláb (angolul: fibre boundle).
Ezt a fogalmat általánosíthatjuk tér-párokra is:
12.3. Definíció (tér-pár nyaláb).
Legyenek (X,A) és (F,B) tér-párok, Y egy topológikus tér, f : X → Y
egy folytonos függvény. Azt mondjuk, hogy
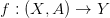 egy (F,B)
egy (F,B)-nyaláb
, ha minden y ∈ Y pontnak van egy y ∈ Uy ⊆
Y környezete, amelyre f−1(U
y) homeomorf (F,B) × Uy-nal. Ha nem
akarjuk hangsúlyozni, hogy mi a rost, akkor egyszerűen egyszerűen tér-pár
nyalábról
.
12.4. Definíció (Rost szorzat). Legyenek X, Y , Z topológikus terek,
f : Y → X és g : Z → X folytonos függvények. Az Y éa Z X feletti
rost-szorzatát így definiáljuk:
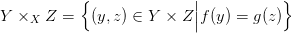 Amennyiben f és g lokálisan triviálisak F és G rosttal (12.2. Definíció),
akkor Y ×XZ is lokálisan triviális F × G rosttal.
Amennyiben f és g lokálisan triviálisak F és G rosttal (12.2. Definíció),
akkor Y ×XZ is lokálisan triviális F × G rosttal.
Nem csak topológikus terekből készíthetünk nyalábokat, hanem szinte
minden geometriai vagy algebrai objektumból is. Erre jó példa a
vektornyaláb fogalma, ahol a rostok vektorterek. Íme, egy másik variáció,
ahol a rostok Abel csoportok, diszkrét topológiával:
12.5. Definíció (Lokális rendszerek). Legyen G egy Abel csoport,
X egy topológikus tér. Lássuk el a G-t a diszkrét topológiával. Egy
G rostú lokális renszer egy γ : Y → X nyaláb G rosttal, amin
értelmezve van egy folytonos Y × XY → Y szorzás (rostonkénti,
12.4. Definíció), és amelyben a γ−1(U)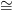 G × U lokális trivializációk
választhatók szorzás-tartó módon. (Ez értelmes, hiszen a G-beli szorzás
ad egy természetes rostonkénti szorzást az G × U → U nyalábon.)
G × U lokális trivializációk
választhatók szorzás-tartó módon. (Ez értelmes, hiszen a G-beli szorzás
ad egy természetes rostonkénti szorzást az G × U → U nyalábon.)
12.6. Megjegyzés. A vektor-nyalábokhoz hasonlóan
a lokális rendszerek is megadhatók áttérési függvényekkel. Itt most
lineáris transzformációk helyett G automorfizmusait kell használni, és
mivel most G topológiája diszkrét, azért az áttérési függvények lokálisan
konstans Aut(G)-értékű függvények.
12.7. Konstrukció. Legye X egy ívszerűen összefüggő, lokálisan
pontrahúzható tér, 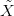 jelöli az univerzális fedőterét. Legyen G egy Abel
csoport, és ϕ : π1(X) → Aut(G) egy csoport homomorfizmus (az ilyen
homomorfizmusokat hívják reprezentációnak). Lássuk el G-t a diszkrét
topológiával! A π1(X) csoport hat az
jelöli az univerzális fedőterét. Legyen G egy Abel
csoport, és ϕ : π1(X) → Aut(G) egy csoport homomorfizmus (az ilyen
homomorfizmusokat hívják reprezentációnak). Lássuk el G-t a diszkrét
topológiával! A π1(X) csoport hat az 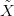 téren és a G csoporton is, tekintsük
a szorzat-hatást az
téren és a G csoporton is, tekintsük
a szorzat-hatást az 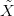 × G téren. A hatás szerinti faktor egy G rostú
nyaláb:
× G téren. A hatás szerinti faktor egy G rostú
nyaláb:
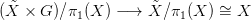 | (2) |
Ráadásul az X × G → X nyaláb a G-koordinátán ható (relatív) szorzással
egy lokális rendszert alkot, és a π1(X)-hatás felcserélhető ezzel a szorzással.
Ezért a szorzás öröklődik a faktor térre is, (2) is egy G rostú lokális
rendszer.
Könnyen látható, hogy pontrahúzható téren minden lokális rendszer
triviális. Ebből következik, hogy minden X fölötti lokális rendszer megkapható
ezzel a konstrukcióval.
12.8. Definíció. Az ℝ rostú
lokális rendszereket lapos vektornyaláboknak hívjuk. Ezek tehát olyan
vektor-nyalábok, amelyek megadhatók konstans áttérési függvényekkel
— de most a rostok (vektorterek) topológiája diszkrét. Egy lapos
nyalábok közti homomorfizmust lapos homomorfizmusnak mondunk, ha
ebben a finomabb topológiában is folytonos — tehát lokálisan konstans
mátrixokkal adható meg.
12.9. Megjegyzés. A 12.7. Konstrukcióban láttuk, hogy az X tér
fölötti r rangú vektornyalábok bijekcióban vannak a π1(X) fundamentális
csoport r-dimenziós (lineáris) reprezentációival.
12.10. Konstrukció (rostonkénti homológia). Legyen (F,B) egy
tér-pár, f : (X,A) → Y egy (F,B)-nyaláb, n ≥ 0 egész szám.
Tegyük fel, hogy Y lokálisan pontrahúzható, megmutatjuk, hogy az
egyes Hn f−1(y); ℤ
f−1(y); ℤ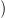 homológia-csoportok (ahol y végigfut Y pontjain)
összeállnak egy lokális rendszerré (12.5. Definíció). Ez az f nyaláb
rostonkénti homológiája,
homológia-csoportok (ahol y végigfut Y pontjain)
összeállnak egy lokális rendszerré (12.5. Definíció). Ez az f nyaláb
rostonkénti homológiája, 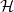 n(f; ℤ).
n(f; ℤ).
A lokális rendszer alaphalmaza, és az Y -ra való vetítése:
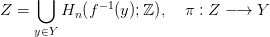
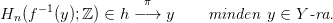 A vetítés rostjai Abel csoportok, izomorfak Hn(F,B; ℤ)-vel. Hátra van
még, hogy topológiát adjunk a Z alaphalmaznak. Legyen U ⊆ Y egy
pontrahúzható nyílt halmaz. Minden y ∈ U pontra az f−1(y) → f−1(U)
beágyazás homotóp ekvivalencia, ez együttvéve kiadnak egy kanonikus
bijekciót:
A vetítés rostjai Abel csoportok, izomorfak Hn(F,B; ℤ)-vel. Hátra van
még, hogy topológiát adjunk a Z alaphalmaznak. Legyen U ⊆ Y egy
pontrahúzható nyílt halmaz. Minden y ∈ U pontra az f−1(y) → f−1(U)
beágyazás homotóp ekvivalencia, ez együttvéve kiadnak egy kanonikus
bijekciót:
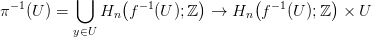 Lássuk el a Hn
Lássuk el a Hn f−1(U); ℤ
f−1(U); ℤ homológia-csoportot a diszkrét topológiával,
π−1(U)-nek pedig adjuk a vele bijekcióban álló H
n
homológia-csoportot a diszkrét topológiával,
π−1(U)-nek pedig adjuk a vele bijekcióban álló H
n f−1(U); ℤ
f−1(U); ℤ × U
szorzat-topológiáját. Ezt minden U ⊆ Y pontrahúzható nyílt halmazzal
elvégezzük. Ez indukál egy topológiát az egész Z halmazon: egy részhalmaz
pontosan akkor zárt, ha π−1(U)-ba eső része zárt minden U ⊆ Y pontrahúzható
nyílt részhalmazra.
× U
szorzat-topológiáját. Ezt minden U ⊆ Y pontrahúzható nyílt halmazzal
elvégezzük. Ez indukál egy topológiát az egész Z halmazon: egy részhalmaz
pontosan akkor zárt, ha π−1(U)-ba eső része zárt minden U ⊆ Y pontrahúzható
nyílt részhalmazra.
12.11. Definíció. Legyen M egy differenciálható sokaság, f : E →
M egy vektornyaláb. Tekintsük a TE, TM érintő-nyalábokat! Az f
differenciálja egy df : TE → f∗TM nyaláb homomorfizmus, a magja
TvE ≤ TE, a vertikális nyaláb. Ehhez választhatunk egy direkt
komplementumot:
 Egy ilyen direkt felbontást
Egy ilyen direkt felbontást konnexiónak
mondunk, ThE a horizontális
nyaláb
(ami persze függ a választásunktól). Több ekvivalens definíciót
találsz még itt.
Egy N ⊂ E részsokaság vízszintes, vagy horizontális, ha TN ≤ ThE,
azaz N minden érintő-vektora vízszintes. Legyen G ⊆ M egy sima görbe és
e ∈ E egy pont amelyre f(e) ∈ G. Picard tétele (differenciálegyenletek
megoldása) miatt létezik (egyetlen) olyan  ⊂ E sima görbe, amely átmegy
az e ponton, és amelyre f(
⊂ E sima görbe, amely átmegy
az e ponton, és amelyre f(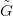 ) = G. Ezt a G felemelésének mondjuk.
Ugyanezt a konstrukciót hívják még párhuzamos eltolásnak is (azaz
) = G. Ezt a G felemelésének mondjuk.
Ugyanezt a konstrukciót hívják még párhuzamos eltolásnak is (azaz 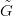 „párhuzamos” G-vel).
„párhuzamos” G-vel).
Legyen most G egy hurok. Az e-ből induló 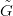 görbe másik végpontja
nem feltétlenül hurok. Most e végigfut a nyaláb megfelelő rostján
(ami egy V vektortér), így sok-sok vízszintes görbét kapunk. Ha a
kezdőpontokhoz hozzárendeljük a végpontokat, akkkor egy V → V
monodrómia transzformációt kapunk. Nem nehéz belátni, hogy ez
egy lineáris transzformáció. Ha most G végigfut az összes f(e)-ből
induló hurkon, akkor az összes így kapott transzformáció egy zárt
részcsoportot alkot GL(V )-ben, ezt hívjuk a konnexió holonómia
csoportjának.
görbe másik végpontja
nem feltétlenül hurok. Most e végigfut a nyaláb megfelelő rostján
(ami egy V vektortér), így sok-sok vízszintes görbét kapunk. Ha a
kezdőpontokhoz hozzárendeljük a végpontokat, akkkor egy V → V
monodrómia transzformációt kapunk. Nem nehéz belátni, hogy ez
egy lineáris transzformáció. Ha most G végigfut az összes f(e)-ből
induló hurkon, akkor az összes így kapott transzformáció egy zárt
részcsoportot alkot GL(V )-ben, ezt hívjuk a konnexió holonómia
csoportjának.
Láttuk, hogy M -beli görbéket mindig fel lehet emelni vízszintesen.
Érdemes megvizsgálni, hogy mi a helyzet magasabb dimenziós
részsokaságokkal:
12.12. Definíció. Legyen M egy n-dimenziós differenciálható
sokaság, E → M egy vektornyaláb. Egy konnexió lapos, ha E minden
pontján keresztül húzható egy n-dimenziós vízszintes részsokaság.
Picard tételének sok-dimenziós változata, a Frobenius tétel. Ennek
segítségével látható, hogy egy konnexió pontosan akkor lapos, ha bármely
két vízszintes vektormező Lie zárójele ismét vízszintes. Ez ekvivalens
azzal, hogy a konnexió konnexió görbülete nulla.
12.13. Megjegyzés. Legyen most E → M egy vektornyaláb egy
lapos konnexióval. Világos, hogy egymással homotóp hurkok vízszintes
felemeltjei is homotópok, tehát a (fent definiált) monodrómia ad egy
π1(M) → GL(V ) reprezentációt, ezt hívjuk
monodrómia reprezentációnak. Ez a reprezentáció ugyanaz, mint amit
a 12.9. Megjegyzésben illetve a 12.7. Konstrukció-ban említünk.
 U : f−1(U) → U megszorítás U felett izomorf az
F × U → U projekcióval. Ezeket az U feletti izomorfizmusokat lokális
trivializációknak hívjuk. Ilyen esetben azt mondjuk, hogy f : Y → X
egy F-nyaláb (angolul: F-bundle), vagy másképpen, F → Y
U : f−1(U) → U megszorítás U felett izomorf az
F × U → U projekcióval. Ezeket az U feletti izomorfizmusokat lokális
trivializációknak hívjuk. Ilyen esetben azt mondjuk, hogy f : Y → X
egy F-nyaláb (angolul: F-bundle), vagy másképpen, F → Y 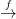 X egy
nyaláb , vagy fibrált nyaláb (angolul: fibre boundle).
X egy
nyaláb , vagy fibrált nyaláb (angolul: fibre boundle).
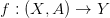
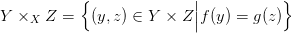
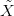
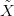
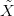
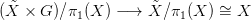

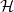
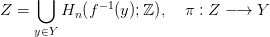
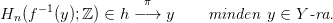
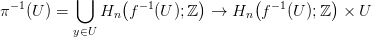

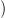

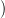

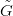
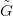
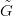 „párhuzamos”
„párhuzamos” 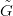 görbe másik végpontja
nem feltétlenül hurok. Most
görbe másik végpontja
nem feltétlenül hurok. Most