13. Fokszám
Ha M egy kompakt (peremes) sokaság, akkor az M∕∂M faktor-térnek
van egy kitüntetett pontja (∂Y képe), melynek komplementuma
egy differenciálható sokaság. Ebben a fejezetben fontos, hogy ilyen
„sokaság-szerű” objektumokkal dolgozzunk, ezért van szükségünk a
következőkre:
13.1. Definíció (Csúcsos sokaság). Egy kompakt csúcsos sokaság
egy X kompakt Hausdorff topológikus tér a következő struktúrával
ellátva:
-
∙
- Egy
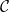 ⊂ X véges részhalmaz, ezek a pontok az X csúcsai (az
üreshalmaz is megengedett),
⊂ X véges részhalmaz, ezek a pontok az X csúcsai (az
üreshalmaz is megengedett),
-
∙
- X∘ = X \
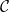 egy differenciálható sokaság (lehet pereme is), ezt az X
sima részének modjuk.
egy differenciálható sokaság (lehet pereme is), ezt az X
sima részének modjuk.
-
∙
- Megköveteljük, hogy X∘ lezártja az egész X legyen, és
-
∙
- X-nek legyen véges sok szimplexből álló szimplex-felbontása.
Az X∘ sima rész peremének lezártját az X peremének hívjuk, ∂X-szel jelöljük.
Ha a perem üres, akkor X egy zárt csúcsos sokaság. Világos, hogy minden
csúcsos sokaság pereme zárt csúcsos sokaság (esetleg csúcs nélkül). Ha
hangsúlyozni akarjuk, hogy X-nek lehet pereme, akkor peremes csúcsos
sokaságnak mondjuk.
Az X csúcsos sokaság szimplex felbontása egy olyan szimplex felbontás,
amelyben a 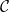 -beli pontok szerepelnek a felbontás csúcsai között, és amelyben
∂X egy rész-komplexus.
-beli pontok szerepelnek a felbontás csúcsai között, és amelyben
∂X egy rész-komplexus.
X egy irányítása nem más, mint az X∘ sima rész irányítása. Ha
rögzítünk egy irányítást X-en, akkor irányított csúcsos sokasággá
válik.
13.2. Példa. Hol találunk csúcsos sokaságokat:
-
(a)
- Minden kompakt differenciálható sokaság egyben csúcsos sokaság is
(nulla csúccsal).
-
(b)
- Ha M egy kompakt sokaság és ∂M≠∅, akkor az M∕∂M faktor-tér
egy csúcsos sokaság. Egy csúcsa van: ∂M képe.
-
(c)
- Még általánosabban, ha X egy n-dimenziós csúcsos sokaság, A ⊊
X egy n-dimenziós kompakt csúcsos részsokaság, akkor az X∕A
faktor-tér is egy csúcsos sokaság. X∕A-nak kétféle csúcsa van:
egyrészt az X∕A-ban lévő csúcsok X∕A-ban is csúcsok maradnak,
másrészt az A képe is csúcs lesz.
13.3. Feladat. Lásd be, hogy egy kompakt csúcsos sokaság minden
csúcsának van olyan környezete, amelyik homeomorf egy peremes
sokaságra állított kúppal! Mi történik, hogy ha a definícióban a véges
szimplex-felbontás helyett ezt a tulajdonságot követeljük meg?
13.4. Feladat. Hogyan definiálnád a (nem feltétlenül kompakt)
csúcsos sokaságokat?
13.5. Definíció (Csúcs-tartó leképezések). Legyenek X, Y csúcsos
sokaságok, f : X → Y egy folytonos függvény, h : X × [0, 1] → Y egy
folytonos homotópia. Jelölje 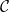 ⊂ X az X csúcsainak halmazát.
⊂ X az X csúcsainak halmazát.
-
∙
- f csúcs-tartó, ha X csúcsait csúcsokba viszi.
-
∙
- f folytonosan differenciálható, ha csúcs-tartó, és folytonosan
differenciálható az Y ∘ sima rész teljes ősképén (ami egy nyílt halmaz
X-ben).
-
∙
- Jelöljük Z-vel az X × [0, 1]
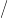
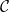 × [0, 1] faktor-teret. Ez is egy csúcsos
sokaság.
× [0, 1] faktor-teret. Ez is egy csúcsos
sokaság.
-
∙
- h csúcs-tartó, ha a
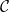 × [0, 1] halmaz minden pontját csúcsba küldi,
azaz indukál egy h : Z → Y csúcs-tartó folytonos függvényt.
× [0, 1] halmaz minden pontját csúcsba küldi,
azaz indukál egy h : Z → Y csúcs-tartó folytonos függvényt.
-
∙
- h folytonosan differenciálható, ha csúcstartó, és az indukált h : Z →
Y leképezés folytonosan differenciálható.
-
∙
- Két X → Y csúcstartó leképezés csúcstartóan homotóp, illetve
folytonosan diferenciálhatóan homotóp, ha van köztük csúcstartó,
illetve folytonosan differenciálható homotópia.
13.7. Tétel (Szimplíciális approximáció). Legyenek X, Y kompakt
csúcsos sokaságok, és f : X → Y egy csúcstartó folytonos leképezés.
-
(a)
- Létezik a két csúcsos sokaságnak olyan szimplex-felbontása (lásd
a 13.1. Definíciót), és hozzá olyan g : X → Y szimplíciális
leképezés, amely csúcstartó, és csúcstartóan homotóp f-fel.
-
(b)
- Legyenek továbbá x1,…,xm ∈ X olyan pontok, melyek
környezetében f folytonosan differenciálható, és a Jakobi
determinánsa nem nulla. Ilyenkor megkövetelhetjük, hogy az
x1,…,xn pontok egy-egy n-szimplex belsejében legyenek, ezeken a
kitüntetett szimplexeken az f és g megegyezzen, sőt, ezeken a
szimplexeken az egész f ∼ g homotópia is triviális legyen.
Emékeztető: egy h : X × [0, 1] → Y homotópia egy U ⊆ X részhalmazon akkor
triviális, ha az (u,t) ∈ U × [0, 1] pontokban h(u,t) csak u-tól függ, t-től
független.
13.8. Definíció (Differenciálható leképezés foka). Legyenek X, Y
n-dimenziós irányított zárt csúcsos sokaságok, f : X → Y egy
folytonosan differenciálható leképezés. Válasszunk olyan y ∈ Y ∘ belső
pontot, amelyik az f-nek reguláris értéke! (Ilyen mindig van a Sard
lemma miatt.) Számoljuk össze az f−1(y) pontjait előjelesen: egy pont
+1-et ér, ha az f Jakobi determinánsa pozitív ebben a pontban, ha pedig
negatív, akkor −1-nek számoljuk. Az így kapott (előjeles) összeg deg(f),
az f foka. (Hamarosan belátjuk, hogy ez nem függ az y választásától.)
Mivel y reguláris érték, azért véges sok ősképe van (tehát véges sok
±1-et kell összeadnunk), és a Jacobi determináns egyikben sem
nulla. Ha x ∈ f−1(y), akkor az f függvény diffeomorfizmus az x
pont egy kis környezete és az y pont egy környezete között. Ha
ez a diffeomorfizmus irányítás-tartó, akkor a Jakobi determináns
előjele pozitív x-ben, ha pedig irányítás-fordító, akkor az előjel
negatív.
13.9. Tétel (Differenciálható leképezés foka). Legyenek X, Y
n-dimenziós irányított zárt csúcsos sokaságok, f : X → Y egy folytonosan
differenciálható leképezés.
-
(a)
- Ha Y összefüggő, akkor f foka nem függ a definícióban választott
reguláris értéktől.
-
(b)
- Tegyük fel, hogy van olyan Z kompakt (n + 1)-dimenziós
irányított csúcsos sokaság, melynek (irányított) pereme éppen
X. Ha f kiterjeszthető egy Z → Y folytonosan differenciálható
függvénnyé, akkor deg(f) = 0.
Bizonyítás. Először az (a) állítással foglalkozunk. Tegyük fel, hogy Y
összefüggő! Legyenek y,z ∈ Y reguláris értékek, jelölje deg y(f) és
deg z(f) a kétféle (y-hoz, illetve z-hez tartozó) fokszámot! Alkalmazzuk
a 13.7. Tételt az f függvényre és az {x1,…,xm} = f−1(y) ∪ f−1(z)
véges ponthalmazra. Ez ad nekük szimplex-felbontásokat X-en és
Y -on, és egy g : X → Y szimplíciális approximációt.
Tekintsünk egy σ ⊆ Y n-szimplexet! A g−1(σ) őskép véges sok
(X-beli) n-szimplexből áll, és ezen szimplexek belsejét g diffeomorfan
képezi le σ belsejére. A 13.8. Definíció analógiájára számoljuk meg
előjelesen a g−1(σ) őskép n-szimplexeit: azok a szimplexek, melyeken g
irányítástartó, +1-et érnek, azok pedig, ahol irányítás-fordító, −1-et.
Az így kapott előjeles összeget deg σ(g)-vel jelöljük.
Világos, hogy ha σy az y-t, tartalmazó n-szimplex, akkor deg σy(g)-t
meghatározó előjeles összeg ugyanaz az összeg, mint amivel deg y(f)-et
számoltuk a 13.8. Definícióban, és ha σz a z-t tartalmazó n-szimplex,
akkor deg z(f) = deg σz(g). Tehát elegendő bebizonyítanunk, hogy
deg σ(g) nem függ a σ szimplextől.
Legyen ϕ a σ egy olyan (n− 1)-dimenziós lapja, amelyik az Y belsejében
van. Jelölje τ ⊆ Y a lap másik oldalán élő n-szimplexet. Világos,
hogy g−1(ϕ) diszjunkt (n − 1)-szimplexekből áll, melyek két-két
X-beli n-szimplexet határolnak, és ezáltal párokba rendezzük a
g−1 σ ∪ τ)-beli n-szimplexeket. Legyen ϕ′⊆ g−1(ϕ) az egyik ilyen
(n − 1)-szimplex. A két szomszédos n-szimplex négyféleképpen
helyezkedhet el:
σ ∪ τ)-beli n-szimplexeket. Legyen ϕ′⊆ g−1(ϕ) az egyik ilyen
(n − 1)-szimplex. A két szomszédos n-szimplex négyféleképpen
helyezkedhet el:
-
∙
- g az egyiket σ-ra képezi, a másikat τ-ba, mindkettőn irányítás-tartó.
-
∙
- g az egyiket σ-ra képezi, a másikat τ-ba, mindkettőn
irányítás-fordító.
-
∙
- g mindkettőt σ-ra képezi, az egyiken irányítás-tartó, a másikon
irányítás-fordító (tehát ϕ′ mentén van egy hajtásvonal).
-
∙
- g mindkettőt τ-ra képezi, az egyiken irányítás-tartó, a másikon
irányítás-fordító (tehát ϕ′ mentén most is van egy hajtásvonal).
Könnyen ellenőrizhetjük, hogy a szimplex-pár mind a négy esetben a
ugyanannyival járul hozzá deg σ(g)-hen mint deg τ(g)-hez. Ez mindegyik
párra érvényes, tehát deg σ(g) = deg τ(g). Mivel Y összefüggő, azért
szomszédos szimplexeken keresztül lépkedve σ-ból bármelyik n-szimplexbe.
Így deg σ(g) nem függ σ-tól sem. Az (a) állítást beláttuk.
A (b) állítás bizonyítása sokkal egyszerűbb. Legyen F : Z → Y a
folytonosan differenciálható kiterjesztés. Válasszunk egy y ∈ Y pontot,
amelyik f-nek és F-nek is reguáris értéke! (Ilyen mindig van a Sard lemma
miatt.) Erre az y-ra alkalmazzuk majd a 13.8. Definíciót. Az inverz
függvény tételből következik, hogy F−1(y) egy egydimenziós peremes
részsokaság X-ben (lásd itt). Mivel X kompakt, azért F−1(y) véges sok
szakasz és véges sok körvonal diszjunkt uniója. A szakaszok ∂Z = X-ből
indulnak és oda térnek vissza, a körvonalak pedig elkerülik X-et. Ezért a
szakaszok párokba rendezik f−1(y) ⊆ X pontjait, a pár egyik tagja mindig
pozitívan, a másik pedig negatívan járul hozzá a deg(f)-et definiáló
összeghez. Tehát f−1(y) pontjai páronként kiejtik egymást, így deg(f) = 0
ebben az esetben. □
13.11. Tétel (Folytonos leképezés foka). Legyenek X, Y n-dimenziós
irányított zárt csúcsos sokaságok, f : X → Y egy folytonos csúcstartó
leképezés.
-
(a)
- A 13.10. Definíció jó: mindig tudunk megfelelő
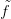 -ot választani,
és minden választás ugyanakkora a fokú.
-ot választani,
és minden választás ugyanakkora a fokú.
-
(b)
- Ha g : X → Y egy olyan folytonos csúcstartó leképezés, amelyik
csúcstartóan homotóp f-fel, akkor deg(f) = deg(g).
-
(c)
- Tegyük fel, hogy van olyan Z (n + 1)-dimenziós irányított
csúcsos sokaság, melynek (irányított) pereme éppen X. Ha f
kiterjeszthető egy Z → Y folytonos csúcstartó függvénnyé, akkor
deg(f) = 0.
Bizonyítás. A 13.6. Tétel miatt van olyan 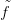 : X → Y folytonosan
differenciálható függvény amelyik csúcstartóan homotóp f-fel. Ha
: X → Y folytonosan
differenciálható függvény amelyik csúcstartóan homotóp f-fel. Ha
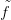 ′ : X → Y egy másik f-fel pontozottan homotóp folytonosan
differenciálható pontozott leképezés, akkor
′ : X → Y egy másik f-fel pontozottan homotóp folytonosan
differenciálható pontozott leképezés, akkor 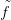 és
és 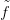 ′ pontozottan
homotópok egymással, tehát 13.6. Tétel miatt van közöttük egy
h : X × [0, 1] → Y folytonosan differenciálható homotópia. Idézzük
fel a 13.5. Definíciót: h indukál egy
′ pontozottan
homotópok egymással, tehát 13.6. Tétel miatt van közöttük egy
h : X × [0, 1] → Y folytonosan differenciálható homotópia. Idézzük
fel a 13.5. Definíciót: h indukál egy 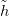 : Z → Y folytonosan
differenciálható függvényt, ahol Z = X ×[0, 1]
: Z → Y folytonosan
differenciálható függvényt, ahol Z = X ×[0, 1]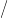
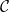 ×[0, 1], és
×[0, 1], és 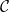 jelöli az
X csúcs-pontjainak halmazát. A 13.9. Tétel miatt a h
jelöli az
X csúcs-pontjainak halmazát. A 13.9. Tétel miatt a h ∂Z megszorítás
foka nulla.
∂Z megszorítás
foka nulla.
Világos, hogy Z pereme az X0 ∨ X1 csokor, ahol X0 = X ×{0},
X1 = X ×{1}, és a felülvonás jelöli az irányítás megfordítását. h
megszorítása X0-ra, illetve X1-re éppen 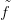 , illetve
, illetve 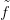 ′. Tehát a fentiek
miatt deg(g) − deg(f) = 0. Ezzel az (a) állítást bebizonyítottuk.
′. Tehát a fentiek
miatt deg(g) − deg(f) = 0. Ezzel az (a) állítást bebizonyítottuk.
A (b) állítás azonnal következik az (a) állításból, hiszen pontosan
ugyanazok a függvények homotópok f-fel mint g-vel.
Legyen F : Z → Y a (c) állításban szereplő függvény. A 13.6. Tétel
alapján választunk egy olyan 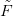 folytonosan diferenciálható függvényt,
amelyik F-fel csúcstartóan homotóp. Világos, hogy az F|X megszorítás
csúcstartóan homotóp f-fel, tehát definíció szerint deg(f) = deg(F|X).
Másrészt, 13.9. Tétel(b) miatt deg(F|X) = 0. Ezzel beláttuk a (c)
állítást is. □
folytonosan diferenciálható függvényt,
amelyik F-fel csúcstartóan homotóp. Világos, hogy az F|X megszorítás
csúcstartóan homotóp f-fel, tehát definíció szerint deg(f) = deg(F|X).
Másrészt, 13.9. Tétel(b) miatt deg(F|X) = 0. Ezzel beláttuk a (c)
állítást is. □
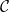 ⊂ X véges részhalmaz, ezek a pontok az X csúcsai (az
üreshalmaz is megengedett),
⊂ X véges részhalmaz, ezek a pontok az X csúcsai (az
üreshalmaz is megengedett),
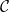 egy differenciálható sokaság (lehet pereme is), ezt az X
sima részének modjuk.
egy differenciálható sokaság (lehet pereme is), ezt az X
sima részének modjuk.
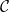 -beli pontok szerepelnek a felbontás csúcsai között, és amelyben
∂X egy rész-komplexus.
-beli pontok szerepelnek a felbontás csúcsai között, és amelyben
∂X egy rész-komplexus.
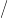
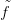

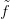
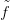
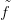
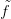
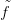
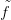
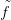 és
és 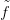
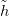
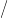

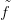 , illetve
, illetve 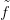
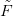 folytonosan diferenciálható függvényt,
amelyik
folytonosan diferenciálható függvényt,
amelyik