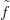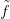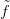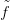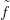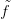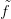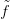14. CW-komplexusok
14.2. Definíció.
-
(a)
- Legyenek X és Y CW-komplexusok. Az X × Y szorzat téren is
van egy cella-felbontás: minden X-beli cellát megszorzunk minden
Y -beli cellával. Ez a cella-felbontás ad egy CW-komplexust,
aminek a topológiája esetleg finomabb, mint a szorzat-topológia.
Ezt az X és az Y CW-szorzatának hívjuk, és X ×CW Y -nal
jelöljük. Lásd még a 14.5. Feladatot és a 14.6. Feladatot!
-
(b)
- Legyenek X és Y CW-komplexusok. Egy f : X → Y folytonos
függvényt CW-függvénynek mondunk (angolul cellular-map), ha
minden n-re az X n-vázát az Y n-vázába viszi.
-
(c)
- Tekintsük [0, 1] intervallumon a következő cella-felbontást: a két
végpont, és az intervallum belseje. Egy X × CW [0, 1] → Y
homotópiát CW-homotópiának hívnk, ha CW-függvény.
-
(d)
- Ha X egy CW-komplexus és A ≤ X egy részkomplexus,
akkor azt mondjuk, hogy (X,A) egy CW-pár. (vesd össze a
11.1. Definícióval). Legyenek (X,A) és (Y,B) CW-párok. Egy
(X,A) → (Y,B) pár-leképezést CW-pár-leképezésnek hívunk,
ha egyúttal CW-leképezés is. Hasonló módon értelmezhető a
CW-pár-homotópia fogalma.
14.3. Definíció. Ebben a jegyzetben Top CW jelöli
a CW-komplexusok kategóriáját a morfizmusok a CW-függvények.
Hasonlóan: Top 2CW jelöli a CW-párok kategóriáját a morfizmusok a
CW-pár-leképezések. (vesd össze a 11.2. Definícióval).
14.4. Megjegyzés. A CW-komplexusokhoz hozzá
tartozik a cella-felbontásuk. Bár ebben a jegyzetben nem foglalkozunk
velük, hasonlóan fontos szerepük van az olyan topológikus tereknek,
amelyek homotóp ekvivalensek egy CW-komplexussal. Ezeknek tehát
nincs rögzített CW felbontásuk. A legtöbb CW-komplexusokra vonatkozó
tétel általánosítható ilyen terekre is.
14.5. Feladat. Legyenek X, Y CW-komplexusok, tegyük fel, hogy az
egyikük lokálisan kompakt. Lásd be, hogy X ×CW Y és X × Y (azaz a
kétféle szorzat-topológia) megegyezik.
14.6. Feladat. Legyenek X, Y CW-komplexusok. Lásd be, hogy az
X ×CW Y 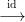 X × Y leképezés egy gyenge homotóp ekvivalencia! Lásd
be, hogy ha X lokálisan kompakt, akkor homeomorfizmus!
X × Y leképezés egy gyenge homotóp ekvivalencia! Lásd
be, hogy ha X lokálisan kompakt, akkor homeomorfizmus!
Ötlet: Dimenzió szerinti indukcióval bizonyítunk. Tegyük fel, hogy az
Xn ≤ X n-vázra igaz az állítás. Ezért az 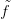 0 függvény és a h homotópia
kiterjeszthetők az Xn ∪ A részkomplexusra. Tekintsük az X egyik
(n + 1)-celláját: ez egy Bn+1 golyó, ∂Bn+1 → X
n ragasztó leképezéssel. A
következő két lépés részleteit az olvasóra hagyjuk:
0 függvény és a h homotópia
kiterjeszthetők az Xn ∪ A részkomplexusra. Tekintsük az X egyik
(n + 1)-celláját: ez egy Bn+1 golyó, ∂Bn+1 → X
n ragasztó leképezéssel. A
következő két lépés részleteit az olvasóra hagyjuk:
14.8. Feladat. Lásd be, hogy az 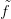 0 függvény és a h homotópia
kiterjeszthetők erre a cellára is.
0 függvény és a h homotópia
kiterjeszthetők erre a cellára is.
14.9. Feladat. Lásd be, hogy az egyes cellákra való kiterjesztések
egymástól függetlenek, összeállnak egy, az egész (n+1)-vázon értelmezett
függvénnyé, illetve homotópiává.
Tehát igaz a tételt az (n + 1)-vázra is. Az 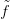 0 függvényt és a h
homotópiát egymás után kiterjesztettük az összes Xn ∪A részkomplexusra
(minden n-re). Ezek uniója az egész X, tehát X-re is igaz a tétel.
□
0 függvényt és a h
homotópiát egymás után kiterjesztettük az összes Xn ∪A részkomplexusra
(minden n-re). Ezek uniója az egész X, tehát X-re is igaz a tétel.
□
14.10. Feladat. Legyenek X és Y CW-komplexusok. Lásd be, hogy
ha az f,g : X → Y CW-függvények homotópok, akkor CW-homotópok
is, sőt, minden f ∼ g homotópia homotóp egy CW-homotópiával!
Ötlet: Használd a 14.7. Tételt! □
14.11. Feladat. Legyenek (X,A) és (Y,B) CW-párok (14.2. Definíció).
Lásd be a következőket:
-
(a)
- Minden (X,A) → (Y,B) pár-leképezés pár-homotóp egy
(X,A) → (Y,B) CW-pár-függvénnyel (lásd a 14.2. Definíciót).
-
(b)
- Ha az f,g : (X,A) → (Y,B) CW-függvények folytonosan
homotópok (mint párok közti leképezések), akkor van köztük
CW-pár-homotópia is (14.2. Definíció).
Ötlet: Használd a 14.7. Tételt! □
14.13. Tétel (Whitehead tétele). Legyenek X, Y CW-komplexusok,
f : X → Y egy gyenge homotópia ekvivalencia. Ekkor f homotóp
ekvivalencia. Tegyük fel, hogy Y az X rész-komplexusa, és f az ebből
adódó beágyazás. Ekkor többet is mondhatunk: Y az X deformációs
retraktuma.
14.14. Feladat. Legyenek X, Y összefüggő CW-komplexusok, f,g :
X → Y folytonos függvények. Fogalmazd meg, és bizonyítsd be
Whitehead tételének (14.13. Tétel) egy olyan változatát, ami azt dönti
el, hogy f és g homotópok-e.
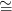 Bn egy golyó,
∂enα
Bn egy golyó,
∂enα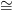 Sn−1 egy gömb, tehát e
nα∕∂e
nα
Sn−1 egy gömb, tehát e
nα∕∂e
nα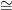 Sn egy gömb, és X
n∕Xn−1 =∨
α
Sn egy gömb, és X
n∕Xn−1 =∨
α enα∕∂e
nα
enα∕∂e
nα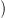
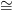 ∨
αSn egy gömbökből álló csokor. Jelölje
∨
αSn egy gömbökből álló csokor. Jelölje
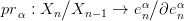
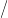 ∂e
nα gömbön az identitás, a csokor összes
többi tagját az enα
∂e
nα gömbön az identitás, a csokor összes
többi tagját az enα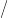 ∂e
nα kitüntetett pontjána viszi.
∂e
nα kitüntetett pontjána viszi.