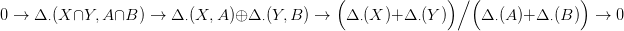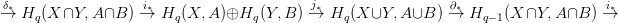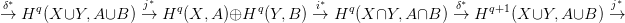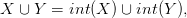
21.1. Tétel (Kivágás). Legyenek A és B olyan részhalmazok az X topológikus térben, melyekre B ⊆ int(A). Ekkor a Δ⋅(X \ B,A \ B) → Δ⋅(X,A) lánc-leképezés egy lánc-ekvivalencia.

21.2. Definíció. Legyenek X, Y egy topológikus tér alterei. Azt mondjuk, hogy {X,Y } jól vág (angolul: excisive), ha

ahol a halmazok belsejét az X∪Y topológiájában számoljuk. Speciálisan, ha Y ⊆ X, akkor {X,Y } jól vág.

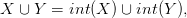
21.3. Lemma. Ha {X,Y } jól vág, akkor az alábbi (szinguláris) lánckomplexusok közti beágyazás lánc-ekvivalencia:

Ebből tenzor-szorzás, illetve a Hom funktor segítségével kapjuk az alábbi lánc-leképezéseket, ezek is lánc-ekvivalenciák. (G tetszőleges abel-csoport.)

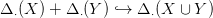
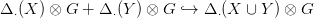
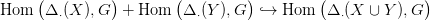
21.4. Feladat. Lásd be a 21.1. Tétel következő általánosítását: ha {X,Y } jól vág jól, akkor (X,X ∩ Y )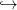(X ∪ Y,Y ) izomorfizmust indukál a szinguláris homológiákon, és kohomológiákon!

21.5. Tétel (Mayer-Vietoris sorozat). Legyenek X,Y,A,B alterek egy topológikus térben, melyekre A ⊆ X és B ⊆ Y . Tegyük fel, hogy {X,Y } és {A,B} jól vágnak. Tekintsük az alábbi funktoriális rövid egzakt sorozat:

Alább láthatók hozzá tartozó hosszú egzakt sorozatok (homológiára és kohomológiára). Tetszőleges együttható-csoporttal (vagy modulussal) érvényesek, az olvashatóság kedvéért az együtthatókat nem tüntettük fel: