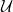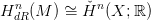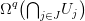20. DeRham kohomológia
20.1. Definíció. Legyen M egy differenciálható sokaság. T∗M jelöli
az érintő nyaláb duálisát — ezt ko-érintő nyalábnak is nevezik, ennek
szelései az 1-formák. ∧
kT∗M jelöli a ko-érintő nyaláb k-adik külső
hatványát — ennek szelései a k-formák. Jelölje Ωk(M) az egész M-en
értelmezett k-formák terét! A külső deriválás minden k-ra egy d :
∧
kTM → ∧k+1T∗M differenciál operátor, tehát egy d : Ωk(M) →
Ωk+1(M) lineáris leképezés ami kielégíti a Leibnitz-szabályt. Érdemes
megemlíteni, hogy d2 = 0, és hogy Ω0(M) nem más, mint az M-en
értelmezett sima függvények tere.
20.2. Definíció. Legyenek M, N differenciálható sokaságok, és f :
M → N egy sima függvény! Jelölje f∗TN az N érintő-nyalábjának
visszahúzottját! Az f deriváltja felfogható egy df : TM → f∗TN
nyaláb-leképezésnek, azaz a Hom  TM,f∗TN
TM,f∗TN nyaláb egy szelésének.
(Lokális koordinátarendszerben ez egy mátrix-értékű függvény: az f
Jacobi-mátrixa.) Ennek a duálisa indukál f∗ : Ωk(N) → Ωk(M)
homomorfizmusokat minden k-ra. (Tehát a differenciál-formákat
„vissza lehet húzni”.)
nyaláb egy szelésének.
(Lokális koordinátarendszerben ez egy mátrix-értékű függvény: az f
Jacobi-mátrixa.) Ennek a duálisa indukál f∗ : Ωk(N) → Ωk(M)
homomorfizmusokat minden k-ra. (Tehát a differenciál-formákat
„vissza lehet húzni”.)
Mézd még meg Stokes tételét!
20.3. Definíció. Legyen M egy differenciálható sokaság. Az alábbi
komplexust de Rham komplexusnak nevezzük:
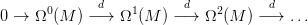 Ez valóban komplexus, hiszen d2 = 0. Az ő k-adik homológiája az M
k-adik
Ez valóban komplexus, hiszen d2 = 0. Az ő k-adik homológiája az M
k-adik de Rham kohomológiája
(ez egy valós vektortér), jelölésben:
HdRk(M). Bővebb információt itt találsz.
20.4. Feladat. Lásd be, hogy Ω⋅ egy kontravariáns funktor a
differenciálható sokaságok (és sima leképezések) kategóriájából a
vektortér komplexusok kategóriájába!
Ötlet. Lásd be, hogy a differenciál-formák visszahúzása kommutál a d
operátorral! □
20.5. Feladat. Legyen M egy sokaság, jelölje Δ⋅diff(M) ≤ Δ
⋅(M)
azt a rész-komplexust, amit a folytonosan differenciálható szinguláris
szimplexek generálnak! Lásd be, hogy a Δ⋅diff(M) ≤ Δ
⋅(M) beágyazás
lánc-ekvivalencia!
Ötlet: Imitáld a 16.7. Lemmát, és a bizonyítását. Ehhez szükséged
lehet a 13.6. Tételre. □
20.7. Tétel (Homotóp invariancia). Legyenek M, N differenciálható
sokaságok, f,g : M → N egymással homotóp sima leképezések. A
hozzájuk tartozó két visszahúzás, f∗,g∗ : Ω⋅(N) → Ω⋅(M), homotóp
ekvivalens.
20.8. Következmény (Poincaré lemma).
Legyen M egy pontrahúzható sokaság, és ϕ ∈ Ωk(M), 1 ≤ k ≤ dim(M),
egy olyan k-forma, amelyre dω = 0 (azaz ω zárt forma). Ekkor van
olyan ψ ∈ Ωk−1(M), amelyre dψ = ϕ (azaz ϕ egzakt forma). Ebből
azonnal következik, hogy az Ω⋅(M) de Rham komplexus pontrahúzható
(2.17. Következmény).
Bizonyítás. Következik a 20.7. Tételből. □
20.9. Feladat (Poincaré lemma változata). Legyen M megint egy
pontrahúzható sokaság, és jelölje ℝM ⊆ Ω0(M) az M → ℝ konstans
függvények halmazát. Mutasd meg, hogy az alábbi sorozat egzakt:
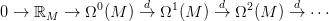
Bizonyítás. Legyen  az M sokaság egy szimplex-felbontása (ilyen
van Whitney tétele miatt), jelöljük
az M sokaság egy szimplex-felbontása (ilyen
van Whitney tétele miatt), jelöljük 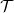 k-val a
k-val a 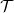 -beli k-szimplexek
halmazát! Vegyük észre, hogy a szimplex-felbontásunk lokálisan véges,
azaz minden pontnak van olyan környezete amelyet csak véges sok
szimplex metsz! Ha a differenciál-formákat csak a
-beli k-szimplexek
halmazát! Vegyük észre, hogy a szimplex-felbontásunk lokálisan véges,
azaz minden pontnak van olyan környezete amelyet csak véges sok
szimplex metsz! Ha a differenciál-formákat csak a 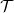 -beli szimplexeken
integráljuk, akkor az
-beli szimplexeken
integráljuk, akkor az  leképezés mintájára egy
leképezés mintájára egy 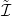 : Ω⋅(M) →
Hom
: Ω⋅(M) →
Hom  Δ⋅szimpl(
Δ⋅szimpl(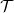 ), ℝ
), ℝ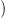 lánc-leképezést. A 20.5. Feladat miatt elég
belátnunk, hogy
lánc-leképezést. A 20.5. Feladat miatt elég
belátnunk, hogy 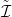 lánc-homotóp-ekvivalencia. Ezért konstruálunk egy
lánc-homotóp-ekvivalencia. Ezért konstruálunk egy
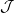 ⋅ : Hom
⋅ : Hom  Δ
⋅szimpl(
Δ
⋅szimpl(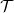 ), ℝ
), ℝ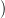 → Ω⋅(M) homotópia inverzet.
→ Ω⋅(M) homotópia inverzet.
Rögzítünk egy k ≥ 0 egészet! Minden σ ∈ 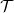 k szimplexhez
választunk egy Uσ ⊆ M nyílt halmazt úgy, hogy mindegyik σ ∈
k szimplexhez
választunk egy Uσ ⊆ M nyílt halmazt úgy, hogy mindegyik σ ∈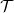 k
metszi Uσ-t, és az Uσ halmazok páronként diszjunktak. Minden σ ∈
k
metszi Uσ-t, és az Uσ halmazok páronként diszjunktak. Minden σ ∈
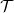 k-ra választunk olyan ψσ ∈ Ωk(M) differenciál-formát, amelyik nulla
az Uσ halmazon kívül, és ∫
σψσ = 1. Ezután minden f : Δk(M) → ℝ
koláncra legyen
k-ra választunk olyan ψσ ∈ Ωk(M) differenciál-formát, amelyik nulla
az Uσ halmazon kívül, és ∫
σψσ = 1. Ezután minden f : Δk(M) → ℝ
koláncra legyen
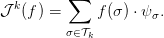
Világos, hogy
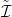

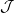 k(f)
k(f)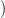 = f
= f. Az is igaz, hogy
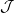 ⋅ ∘
⋅ ∘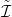
homotóp az
identitáshoz (az
Ω⋅(M) komplexuson), de azt most nem bizonyítjuk.
□
Bizonyítás. A azonnal következik a 3.24. Következményből, csak a
megfelelő kettős komplexust kell kitölteni — amit az olvasóra bízunk!
□
20.12. Feladat. Töltsd ki az előző bizonyítás végén felbukkanó kettős
komplexust! Lásd be, hogy a sorok és az oszlopok valóban egzaktak!
Ötlet: Minden (p + 1)-elemű J ⊆ I részhalmazhoz készítsd el a
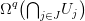
csoportot. Ezek direkt szorzata legyen a
3.24. Következményben keresett
Mp,q csoport! A
q irányban a differenciál legyen a differenciál formák
d
operátora. A
p iránban pedig imitáld a Čech komplexus differenciálját!
Minden
q irányú oszlop DeRham komplexusok direkt szorzata, az egzaktság
a Poincaré lemmából következik. Tekints egy
p irányú sort, egység-osztás
segítségével lásd be, hogy pontrahúzható (
2.17. Következmény). Ebből
következik a
p irányú egzaktság.
□
20.13. Feladat (de Rham tétel másik bizonyítása). Lásd be a
20.10. Tételt a 20.11. Tétel és a 19.5. Tétel segítségével.
20.14. Feladat (de Rham tétel harmadik bizonyítása). Lásd be a
Mayer-Vietoris tétel (21.5. Tétel) de Rham kohomológiára vonatkozó
változatát! Mutasd meg, hogy ebből is következik a 20.10. Tétel!
 TM,f∗TN
TM,f∗TN nyaláb egy szelésének.
(Lokális koordinátarendszerben ez egy mátrix-értékű függvény: az f
Jacobi-mátrixa.) Ennek a duálisa indukál f∗ : Ωk(N) → Ωk(M)
homomorfizmusokat minden k-ra. (Tehát a differenciál-formákat
„vissza lehet húzni”.)
nyaláb egy szelésének.
(Lokális koordinátarendszerben ez egy mátrix-értékű függvény: az f
Jacobi-mátrixa.) Ennek a duálisa indukál f∗ : Ωk(N) → Ωk(M)
homomorfizmusokat minden k-ra. (Tehát a differenciál-formákat
„vissza lehet húzni”.)
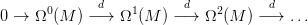


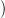

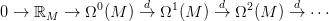

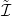

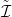 lánc-homotóp-ekvivalencia. Ezért konstruálunk egy
lánc-homotóp-ekvivalencia. Ezért konstruálunk egy
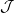

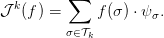

 homotóp az
identitáshoz (az
homotóp az
identitáshoz (az