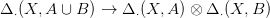22.1. Tétel (Eilenberg-Zilber). Legyenek X,Y tópologikus terek. Létezik egy
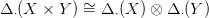
22.1. Tétel (Eilenberg-Zilber). Legyenek X,Y tópologikus terek. Létezik egy
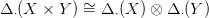
Bizonyítás. Ha A és B CW-komplexusok, akkor
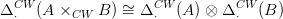 | (5) |
kanonikusan izomorf (14.2. Definíció). Ezt az azonosságot az A = S(X) és a B = S(Y ) CW-komplexusokra akarjuk alkalmazni. X gyengén homotóp ekvivalens az S(X) CW-komplexussal (lásd a 16.5. Tételt), Y gyengén homotóp ekvivalens S(Y )-nal, ezért aztán X × Y gyengén homotóp ekvivalens az S(X) × S(Y ) szorzattal, ami viszont gyengén homotóp ekvivalens az S(X) ×CW S(Y ) CW-szorzattal (14.6. Feladat). Ezért a tétel következik az (5) azonosságból. □
22.2. Következmény. Legyenek (X,A) és (Y,B) olyan tér-párok (11.1. Definíció), melyekre {X × B,A × Y } jól vág (21.2. Definíció). Ekkor van egy természetes lánc-ekvivalencia:
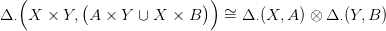
22.3. Feladat. Igazold a (6) azonosságot!
22.4. Megjegyzés. Érdekes az analógia van a szabad algebrák és az
alábbi tétel között. Adott algebrai struktúrák egy 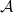 osztálya és egy
X halmaz. Az X által generált szabad algebra egy olyan FX ∈
osztálya és egy
X halmaz. Az X által generált szabad algebra egy olyan FX ∈ 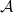 algebra, amely tartalmazza X-et, és tetszőleges A ∈
algebra, amely tartalmazza X-et, és tetszőleges A ∈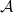 algebrába képező
tetszőleges X → A függvény egyértelműen kiterjeszthető egy Fx →
A homomorfizmussá. Az X halmazt hívjuk az FX szabad generátor
rendszerének. Az FX szabad algebra, ha létezik, izomorfizmus erejéig
egyértelmű, csak az X számosságától függ (meg persze
algebrába képező
tetszőleges X → A függvény egyértelműen kiterjeszthető egy Fx →
A homomorfizmussá. Az X halmazt hívjuk az FX szabad generátor
rendszerének. Az FX szabad algebra, ha létezik, izomorfizmus erejéig
egyértelmű, csak az X számosságától függ (meg persze 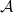 -tól). Szép
-tól). Szép
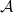 osztály esetén (pl. ha
osztály esetén (pl. ha 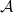 -t azonosságokkal definiáljuk) a létezése is
könnyen bizonyítható.
-t azonosságokkal definiáljuk) a létezése is
könnyen bizonyítható.
Tekintsük a „pozitív dimenzióban aciklikus” funktorok világát. Az alábbi tételünk arról szól, hogy Δ⋅ „szabad funktor”-ként működik ebben a világban, H0(Δ⋅) játssza a „szabad generátor rendszer” szerepét. A bizonyítás még hangsúlyosabbá teszi az analógiát: az aciklikusságot „azonosság”-ként értelmezzük.
22.5. Tétel (Eilenberg, aciklikus modellek módszere).
Legyen 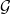 ⋅ egy funktor, ami topológikus terekhez komplexusokat rendel
(és folytonos függvényekhez lánc-homomorfizmusokat). Tegyük fel, hogy
⋅ egy funktor, ami topológikus terekhez komplexusokat rendel
(és folytonos függvényekhez lánc-homomorfizmusokat). Tegyük fel, hogy
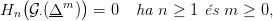

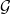 ⋅(X)
⋅(X)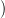 természetes transzformáció
egy (X-től függő) természetes τ⋅ : Δ⋅ →
természetes transzformáció
egy (X-től függő) természetes τ⋅ : Δ⋅ → 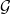 ⋅
lánc-homomorfizmusból származik: t = H0(τ⋅).
⋅
lánc-homomorfizmusból származik: t = H0(τ⋅).
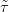 ⋅ : Δ⋅ →
⋅ : Δ⋅ → 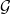 ⋅ egy
másik természetes lánc-homomorfizmus amire H0(τ⋅) = H0(
⋅ egy
másik természetes lánc-homomorfizmus amire H0(τ⋅) = H0(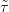 ⋅),
akkor τ⋅ és
⋅),
akkor τ⋅ és 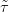 ⋅ lánc-homotópok egy D⋅ (X-től függő) természetes
lánc-homotópiával.
⋅ lánc-homotópok egy D⋅ (X-től függő) természetes
lánc-homotópiával.
22.6. Feladat. Lásd be, hogy H0 Δ⋅(X)
Δ⋅(X)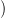 kanonikusan izomorf az X
összefüggő komponenzei által szabadon generált szabad Abel csoporttal.
Konstruálj ez alapján egy H0(Δ⋅) → H0(Δ⋅) ⊗ H0(Δ⋅) természetes
transzformációt!
kanonikusan izomorf az X
összefüggő komponenzei által szabadon generált szabad Abel csoporttal.
Konstruálj ez alapján egy H0(Δ⋅) → H0(Δ⋅) ⊗ H0(Δ⋅) természetes
transzformációt!
22.7. Következmény. Létezik egy olyan Δ⋅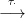 Δ⋅⊗Δ⋅ természetes
transzformáció, amire H0(τ⋅) éppen a 22.6. Feladat természetes
transzformációja, és bármely két ilyen transzformációt összeköt egy
természetes lánc-homotópia.
Δ⋅⊗Δ⋅ természetes
transzformáció, amire H0(τ⋅) éppen a 22.6. Feladat természetes
transzformációja, és bármely két ilyen transzformációt összeköt egy
természetes lánc-homotópia.
Bizonyítás. A 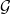 ⋅ = Δ⋅⊗ Δ⋅ funktor kielégíti a 22.5. Tétel feltételeit.
□
⋅ = Δ⋅⊗ Δ⋅ funktor kielégíti a 22.5. Tétel feltételeit.
□
22.8. Konstrukció. Az alábbi diagramon δ jelöli az X → X × X átló-leképezést, EZ pedig az Eilenberg-Zilber tételben (22.1. Tétel) szereplő lánc-ekvivalenciát, τ⋅ pedig a két másik lánc-homomorfizmus kompozíciója:
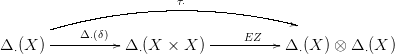
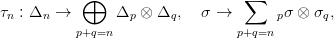
 pσ
pσ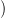 =
p, dim
=
p, dim  σq
σq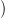 = q, és a két lapnak egyetlen közös csúcsa van: a (p +
1)-edik. A két konstrukció természetesen különböző τ⋅ lánc-homomorfizmusokat
ad, de a 22.7. Következmény miatt ezek lánc-homotópok.
= q, és a két lapnak egyetlen közös csúcsa van: a (p +
1)-edik. A két konstrukció természetesen különböző τ⋅ lánc-homomorfizmusokat
ad, de a 22.7. Következmény miatt ezek lánc-homotópok.
22.9. Feladat. Tekintsük a 22.8. Konstrukciót.
22.10. Tétel. Legyn τ⋅ a 22.7. Következménybeli lánc-homomorfizmus!
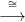 Δ⋅(X)⊗Δ⋅(X) az x⊗y → y⊗x
szimmetriát. Az alábbi kompozíció lánc-homotóp τ⋅-val:
Δ⋅(X)⊗Δ⋅(X) az x⊗y → y⊗x
szimmetriát. Az alábbi kompozíció lánc-homotóp τ⋅-val:
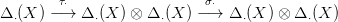
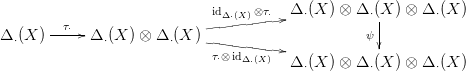
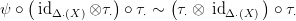
Bizonyítás. Mindkét állítás azonnal következik a 22.5. Tételből. □
22.11. Feladat. Tekintsük az olyan (X,A,B) hármasok kategóriáját, amelyekben X topológikus tér, A,B ⊆ X, és {A,B} jól vágnak.