Ötlet: Keress CW-felbontást, amelyben egy csúcs, 2g él és egy 2-cella van! Az ehhez tartozó lánc-komplexus:
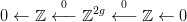
Ötlet: Keress CW-felbontást, amelyben egy csúcs, 2g él és egy 2-cella van! Az ehhez tartozó lánc-komplexus:
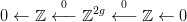
30.3. Feladat. Számítsd ki a nem irányítható felületek ℤ2-együtthatós homológia- és kohomológia-csoportjait!
30.4. Feladat. Számítsd ki a nem irányítható felületek ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.5. Feladat. Számítsd ki az n-dimenziós tórusz ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.6. Feladat. Legyen F egy g nemű felület! Számítsd ki az S1 × F sokaság ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.7. Feladat. Legyenek F és G irányítható felületek! Számítsd ki az F × G sokaság ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.8. Feladat. Legyen F egy g nemű felület, ϕ : F → F egy diffeomorfizmus! Tekintsük az F × [0, 1] hengert! Ragasszuk össze az alaplapját, F ×{0}-t, a fedőlapjával, F ×{1}-gyel a ϕ leképezés mentén (azaz úgy, hogy minden f ∈ F-re az f × 0 pontot a ϕ(f) × 1 ponttal azonosítjuk)! Számítsd ki az így kapott sokaság ℤ-együtthatós homológia és kohomológia-csoportjait!
Eredmény: A lánc-komplexus ekvivalens a következővel:
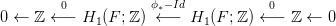
 ℤ2g, ϕ
∗ jelöli a ϕ által indukált H1(F; ℤ) → H1(F; ℤ)
leképezést, Id pedig az identitást. □
ℤ2g, ϕ
∗ jelöli a ϕ által indukált H1(F; ℤ) → H1(F; ℤ)
leképezést, Id pedig az identitást. □
30.9. Feladat. Bontsd fel az S3 gömböt két tömör tórusz uniójára! Írd fel az erre vonatkozó Mayer-Vietoris sorozatot! Számold ki ebből az S3 homológiáit!
30.10. Feladat. Bontsd fel az S1 × S2 sokaságot két tömör tórusz uniójára! Írd fel az erre vonatkozó Mayer-Vietoris sorozatot! Számold ki ebből az S1 × S2 homológiáit!
30.11. Feladat. Legyen A és B két tömör tórusz, és ϕ : ∂A → ∂B egy diffeomorfizmus! Ragasszuk össze a két tömör tórusz peremét a ϕ leképezés mentén, így egy háromdimenziós irányítható sokaságot kapunk! Mutasd meg, hogy a ragasztás megadható egy ϕ∗ : ℤ2 → ℤ2 izomorfizmus segítségével! Hányféle ragasztás lehetséges? Írd fel a ragasztásra vonatkozó Mayer-Vietoris sorozatot! Mennyire határozza meg a kapott sokaság homológiáit!
30.12. Feladat. Bontsd fel az S3 gömböt két tömör g-nemű test uniójára! Írd fel az erre vonatkozó Mayer-Vietoris sorozatot! Számold ki ebből az S3 homológiáit!
30.13. Feladat (Heegaard felbontás). Legyen F ⊂ ℝ3 egy beágyazott g nemű felület. Az F két részre vágja a teret, jelöljük A-val a korlátos részt. Ragasszuk össze az A két példányát a peremeűk mentén egy ϕ : F → F egy diffeomorfizmussal, így egy háromdimenziós sokaságot kapunk. Jelölje ϕ∗ : H1(F; ℤ) → H1(F; ℤ) az indukált homomorfizmust! Írd fel a ragasztásra vonatkozó Mayer-Vietoris sorozatot! Mennyire határozza meg a sokaság homológia csoportjait?
30.14. Megjegyzés. Minden irányítható háromdimenziós sokaság megkapható a 30.13. Feladatban leírt módon, azaz felbontható két tömör g-nemű test uniójára. Az ilyen felbontást Heegaard felbontásnak hívják.
30.15. Feladat. Legyen M egy háromdimenziós sokaság, F egy g nemű felület, és f : M → F egy olyan sima leképezés, amelynek sehol sem nulla a deriváltja, és minden F-beli pont ősképe egy körvonal. (Ezt hívjuk kör-nyalábnak.) Bontsd fel F-et 2g körvonal és egy körlap (pontosabban: egy 4g oldalú sokszög belseje) uniójára! Ez indukál az M sokaságon is egy felbontást. Írd fel az ehhez tartozó Mayer-Vietoris sorozatot! Mennyire határozza meg a sokaság homológia csoportjait? Milyen homológia-homomorfizmus fogja elkódolni a ragasztási információt?
30.16. Feladat. Tekintsük egy dodekaéder két szemközti oldalát: ezek
párhuzamos síkban, 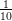 fordulattal elfordított állású szabályos ötszögek.
Azonosítsuk a két ötszög pontjait úgy, hogy minden pontot a szemközti
oldalon neki megfelelő,
fordulattal elfordított állású szabályos ötszögek.
Azonosítsuk a két ötszög pontjait úgy, hogy minden pontot a szemközti
oldalon neki megfelelő, 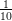 fordulattal elforgatott ponttal azonosítunk!
Ismételjük meg ezt az azonosítást mind a hat szemköztes oldalpárra. Az
így kapott 3-dimenziós sokaság a Poincaré homológia gömb. Számítsd
ki a ℤ-együtthatós homológia- és kohomológia-csoportjait!
fordulattal elforgatott ponttal azonosítunk!
Ismételjük meg ezt az azonosítást mind a hat szemköztes oldalpárra. Az
így kapott 3-dimenziós sokaság a Poincaré homológia gömb. Számítsd
ki a ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.17. Feladat. Legyen G ≤ SO(3) a szabályos dodekaéder forgás-szimmetriáinak csoportja! Lásd be, hogy az SO(3)∕G sokaság diffeomorf a 30.16. Feladatban megkonstruált Poincaré homológia gömbbel. Számítsd ki a homotópia csoportjait!
Ötlet: A Poincaré homológia gömb univerzális fedőtere S3. □
30.18. Feladat. Módosítsd a 30.16. Feladatbeli konstrukciót úgy,
hogy azonosításkor 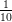 fordulat helyett
fordulat helyett 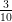 fordulatot használsz! Az így
kapott 3-sokaságot Seifert-Weber sokaságnak hívják. Számítsd ki a
ℤ-együtthatós homológia- és kohomológia-csoportjait!
fordulatot használsz! Az így
kapott 3-sokaságot Seifert-Weber sokaságnak hívják. Számítsd ki a
ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.19. Feladat. A Seifert-Weber sokaság univerzális fedőtere a 3-dimenziós Bolyai-geometria (lásd itt). Számítsd ki a Seifert-Weber sokaság homotópia csoportjait!
30.20. Feladat. Módosítsd a 30.16. Feladatbeli konstrukciót úgy,
hogy azonosításkor 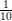 fordulat helyett
fordulat helyett 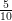 =
= 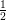 fordulatot használsz!
Lásd be, hogy az így kapott sokaság éppen ℝℙ3. Ez a konstrukció
megadja a projektív tér egy CW-felbontását (nem a szokásosat).
Számítsd ki a felbontáshoz tartozó ℤ-együtthatós CW-homológia-
és CW-kohomológia-csoportokat! Számítsd ki a felbontáshoz tartozó
ℤ2-együtthatós CW-homológia- és CW-kohomológia-csoportokat is!
fordulatot használsz!
Lásd be, hogy az így kapott sokaság éppen ℝℙ3. Ez a konstrukció
megadja a projektív tér egy CW-felbontását (nem a szokásosat).
Számítsd ki a felbontáshoz tartozó ℤ-együtthatós CW-homológia-
és CW-kohomológia-csoportokat! Számítsd ki a felbontáshoz tartozó
ℤ2-együtthatós CW-homológia- és CW-kohomológia-csoportokat is!
30.21. Feladat. Legyenek p,q relatív prím pozitív egészek! Osszuk
a háromdimenziós golyó peremét két félgömbre: É jelöli az északi (zárt)
félgömböt, D pedig a délit. Tekintsük azt a ϕ : É → D leképezést, amelyik
először elforgatja az É félgömböt a tengelye körül 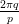 szöggel, majd
tükrözi a határoló kör síkjára. Azonosítsunk minden x ∈É pontot a neki
megfelelő ϕ(x) ∈ D ponttal! Az így kapott sokaság az L(p,q) Lencse
tér. Számítsd ki a ℤ-együtthatós homológia- és kohomológia-csoportjait!
szöggel, majd
tükrözi a határoló kör síkjára. Azonosítsunk minden x ∈É pontot a neki
megfelelő ϕ(x) ∈ D ponttal! Az így kapott sokaság az L(p,q) Lencse
tér. Számítsd ki a ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.22. Feladat. Legyen S3 ⊂ ℂ2 az egységgömb a komplex síkon. Jelölje x,y a koordinátákat ℂ2-en. Tekintsük a
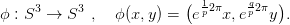
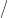 ℤ
p diffeomorf az L(p,q) lencse
térrel (lásd a 30.21. Feladatot)! Számítsd ki a Lencse-tér homotópia
csoportjait!
ℤ
p diffeomorf az L(p,q) lencse
térrel (lásd a 30.21. Feladatot)! Számítsd ki a Lencse-tér homotópia
csoportjait!
Ötlet: A konstrukcióból következik, hogy a Lencse tér univerzális fedőtere a gömb. □
30.24. Feladat. Két tömör tórusz peremét azonosítjuk egy homeomorfizmussal. Mutasd meg, hogy így egy lencse teret kapunk! Mutasd meg, hogy minden lencse tér megkapható ezzel a konstrukcióval!
30.25. Feladat. A 30.24. Feladatban az L(p,q) lencs teret felbontottuk két tömör tórusz uniójára. Írd fel a felbontáshoz tartozó Mayer-Vietoris sorozatokat! Számítsd ki ezek segítségével a lencse terek ℤ-együtthatós homológia- és kohomológia-csoportjait!
30.26. Feladat. Szférikus 3-sokaságnak hívjuk azokat az irányítható sokaságokat, amelyek univerzális fedőtere S3. Tehát a szférikus sokaságok S3∕G alakban írhatók, ahol G ≤ SO(4) egy olyan véges részcsoport, amelyik fixpont-mentesen hat az S3 egység-gömbön! A wikipedia-n megtalálod az összes szóba jövő részcsoportot. Számítsd ki a szférikus sokaságok ℤ-együtthatós homológia- és kohomológia-csoportjait!.