29.1. Tétel (Poincaré dualitás). Legyen M
egy n-dimenziós összefügő, irányítható, zárt topológikus sokaság. Ekkor
Hn(M; ℤ)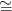 ℤ, és az [M] ∈ Hn(M; ℤ) generátorral való sapka-szorzás
izomorfizmus minden dimenzióban:
ℤ, és az [M] ∈ Hn(M; ℤ) generátorral való sapka-szorzás
izomorfizmus minden dimenzióban:
![k ∼=
D [M ] : H (M ;ℤ) −→ Hn −k(M ;ℤ), D [M](x) = x ∩ [M ]](algebrai-topologia513x.png)
Ennek a fejezetnek a célja, hogy bebizonyítsuk a következőt:
29.1. Tétel (Poincaré dualitás). Legyen M
egy n-dimenziós összefügő, irányítható, zárt topológikus sokaság. Ekkor
Hn(M; ℤ)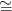 ℤ, és az [M] ∈ Hn(M; ℤ) generátorral való sapka-szorzás
izomorfizmus minden dimenzióban:
ℤ, és az [M] ∈ Hn(M; ℤ) generátorral való sapka-szorzás
izomorfizmus minden dimenzióban:
![k ∼=
D [M ] : H (M ;ℤ) −→ Hn −k(M ;ℤ), D [M](x) = x ∩ [M ]](algebrai-topologia513x.png)
Ebben a fejezetben csupa olyan állítással találkozunk, ami egy kis gömb környezetében könnyen kiszámolható. A fő bizonyítási módszerünk a Mayer-Vietoris sorozat (21.5. Tétel), ennek segítségével tudunk nagy kompakt halmazok környezetéről információt szerezni. A módszerünk a lelke mélyén véges, nem tudunk a kompakt halmazoktól elszabadulni. Ezért van szükségünk a kompakt tartójú kohomológia fogalmára.
Legyen M egy topológikus sokaság, K ⊆ M egy kompakt részhalmaz. A
Hom  Δ⋅(X), ℤ
Δ⋅(X), ℤ komplexusban keresünk olyan rész-komplexust, amelyik a
K halmaz környezetére „koncentrál”. Ha csak olyan koláncokat engedünk
meg, amelyek minden K-ból kilógó szimlexen nullák, akkor nem kapunk
rész-komplexust: egy ilyen kolánc kohatárában szerepelhet egy csomó olyan
szimplex, amelynek csak az egyik oldala van K-ban. Ehelyett csak azt
követeljük majd meg a koláncainktól, hogy a K-tól diszjunkt szimplexeken
nullák legyenek.
komplexusban keresünk olyan rész-komplexust, amelyik a
K halmaz környezetére „koncentrál”. Ha csak olyan koláncokat engedünk
meg, amelyek minden K-ból kilógó szimlexen nullák, akkor nem kapunk
rész-komplexust: egy ilyen kolánc kohatárában szerepelhet egy csomó olyan
szimplex, amelynek csak az egyik oldala van K-ban. Ehelyett csak azt
követeljük majd meg a koláncainktól, hogy a K-tól diszjunkt szimplexeken
nullák legyenek.
29.2. Definíció. Legyen X egy tetszőleges topológikus tér. A kompakt tartójú kohomológiáit így definiáljuk:
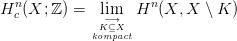
Az alábbi tétel megmutatja, hogy miért nem definiáljuk a „kompakt tartójú homológiákat”: a homológia-osztályok már maguktól kompakt tartójúak.
29.3. Tétel. Legyen X tetszőleges topológikus tér, és A ⊆ X egy altér. Az alábbi izomorfizmusra úgy szokás hivatkozni, hogy „a homológiának kompakt tartója van”. A képletbeben (K,B) a kompakt párokon fut (lásd a 11.3. Definíciót).
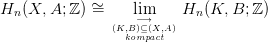
Ötlet: A tétel azért igaz, mert a direkt limesz funktor egzakt. Az analóg állítás kohomológiákra nem igaz, mert az inverz limesz funktor nem egzakt. □
29.4. Konvenció. Legyen M egy topológikus sokaság, K ⊆ M
egy kompakt részhalmaz. Legyen U a K olyan nyílt környezete,
melynek a K deformációs retraktuma. Ha az M viselkedését akarjuk
megérteni a K környezetében, akkor elég az  U,∂U
U,∂U párt (és benne
K-t) tanulmányozni. De
párt (és benne
K-t) tanulmányozni. De  U,∂U
U,∂U homotóp ekvivalens
homotóp ekvivalens  M,M \U
M,M \U -val,
sőt (M,M \ K)-val is. Ezért ebben a fejezetben gyakran dolgozunk
-val,
sőt (M,M \ K)-val is. Ezért ebben a fejezetben gyakran dolgozunk
 M,M \ K
M,M \ K alakú párokkal, érdemes egy jelölést is bevezetni:
alakú párokkal, érdemes egy jelölést is bevezetni:


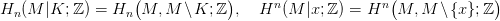
Az alábbi lemma arról szól, hogy egy topológikus sokaságban bármely pont környezetében „lokálisan” érvényes a Poincaré dualitás. Később, a Poincaré dualitás bizonyításakor ezeket a lokális dualitásokat fogjuk majd a Mayer-Vietoris sorozat segítségével összeragasztani.
29.5. Lemma. Legyen M egy n-dimenziós topológikus sokaság, x ∈ M egy pont és B ⊆ M egy x-et tartalmazó tömör golyó. Lásd be, hogy
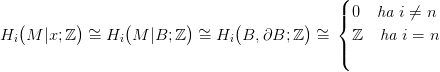
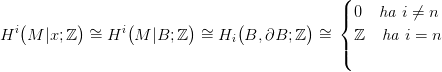
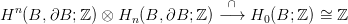
Bizonyítás. A három szóban forgó tér-pár szinguláris lánc-komplexusa lánc-homotóp a kivágási tétel (21.1) miatt:
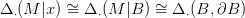
(Az n < 2 eset is nagyon hasonló, az olvasóra hagyjuk). Világos, hogy B CW-lánc-komplexusa n, n − 1 és 0 dimenzióban él:
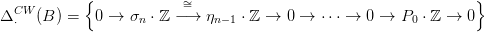
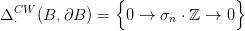
 B × B,B × ∂B
B × B,B × ∂B , és
íme a (B,∂B)
, és
íme a (B,∂B)
 B × B,B × ∂B
B × B,B × ∂B átlós beágyazáshoz tartozó
lánc-homomorfizmus:
átlós beágyazáshoz tartozó
lánc-homomorfizmus:
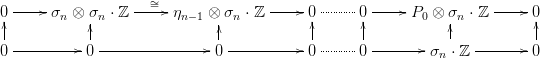
A Poincaré dualitásban kulcs-szerepe van az irányításnak. Klasszikusan az érintő nyaláb segítségével szokás definiálni. Topológikus sokaságokra ez az út nem járható, de van egy jó helyettesítő eszköz: az irányítás nyaláb. A definíció előtt szükség van néhány alapfogalomra.
Legyen M egy n-dimenziós topológikus sokaság, x ∈ M egy pont. Találhatunk egy x ∈ Ux ⊆ M környezetet, amelyik homeomorf az n-dimenziós golyóval. Ha ezeket az Ux környezeteket sikerülne össze-barkácsolni egy golyó-nyalábbá, akkor azt használhatnánk az M érintő-nyalábjának. Ezt sajnos nem tudjuk megtenni, de legalább imitáljuk: Ux helyett megelégszünk az (Ux,∂Ux) párral, ami homotóp ekvivalens az (M|x) párral (29.4. Konvenció). Ha M összefüggő, akkor ezek összeállnak egy tér-pár nyalábbá — amit majd ugyanúgy használunk, mintha ő lenne az éritő-nyaláb.
29.6. Lemma. Legyen M egy összefüggő topológikus sokaság, D ⊆ M×M az átló. Ekkor M homogén a következő értelemben: Bármely két x,y ∈ M pontra M \{x} homeomorf M \{y}-nal. Az alábbi diagramon az M × M direkt szorzat vetítése látható a második tényezőre:
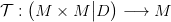
29.7. Megjegyzés. Legyen M egy n-dimenziós topológikus sokaság.
Egy x ∈ M pontban kétféleképpen irányíthatjuk: az irányítást
reprezentálhatjuk ppéldául a Hn M|x; ℤ
M|x; ℤ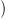 csoport két generátorával
(azaz kétféle képpen azonosíthatjuk Z-vel). Ez analóg azzal, hogy
differenciálható sokaságokon az irányítást megadhatjuk térfogati
formával. A differenciálható esetben tehát az ∧
nT∗M a kulcs az
irányításhoz. Ennek az analógja az alábbi irányítás nyaláb.
csoport két generátorával
(azaz kétféle képpen azonosíthatjuk Z-vel). Ez analóg azzal, hogy
differenciálható sokaságokon az irányítást megadhatjuk térfogati
formával. A differenciálható esetben tehát az ∧
nT∗M a kulcs az
irányításhoz. Ennek az analógja az alábbi irányítás nyaláb.
29.8. Definíció (irányítás nyaláb). Legyen M egy n-dimenziós
topológikus sokaság. A 29.6. Lemma megad minden Mi ⊆ M összefüggő
komponensen egy-egy 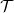 i tér-pár nyalábot. A
i tér-pár nyalábot. A 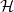 (
(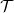 i; ℤ) rostonkénti
homológia (12.10. Konstrukció) egy ℤ-nyaláb az Mi komponensen, ezek
együttvéve egy ℤ-nyalábot alkotnak az egész M-en. Ezt nevezzük az M
irányítás nyalábjának.
i; ℤ) rostonkénti
homológia (12.10. Konstrukció) egy ℤ-nyaláb az Mi komponensen, ezek
együttvéve egy ℤ-nyalábot alkotnak az egész M-en. Ezt nevezzük az M
irányítás nyalábjának.
29.9. Definíció. Legyen M egy n-dimenziós topológikus sokaság,  az irányítás nyalábja, K ⊆ M egy kompakt részhalmaz. Hn(M|K)
elemeit megszorítjuk Hn(M|x)-re, ahol x végigfut K pontjain. Így
minden Hn(M|K)-beli homológia-osztályhoz egy K →
az irányítás nyalábja, K ⊆ M egy kompakt részhalmaz. Hn(M|K)
elemeit megszorítjuk Hn(M|x)-re, ahol x végigfut K pontjain. Így
minden Hn(M|K)-beli homológia-osztályhoz egy K →  folytonos
szelést rendeltünk. Ez a hozzárendelés egy természetes homomorfizmus:
folytonos
szelést rendeltünk. Ez a hozzárendelés egy természetes homomorfizmus:
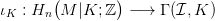
29.10. Lemma. Legyen M egy n-dimenziós topológikus sokaság,  az irányítás nyalábja. Ekkor minden A ⊆ M kompakt részhalmazra
Hi(M|A, ℤ) = 0 ha i > n, és a 29.9. Definícióbeli ιA izomorfizmus.
az irányítás nyalábja. Ekkor minden A ⊆ M kompakt részhalmazra
Hi(M|A, ℤ) = 0 ha i > n, és a 29.9. Definícióbeli ιA izomorfizmus.
Bizonyítás. Ebben a bizonyításban egész együtthatós homológiát használunk, elhagyjuk a ℤ-t a jelölésből. Először belátjuk a következő redukciós lépést: ha az A, B, A ∩ B halmazok teljesítik a lemma feltételeit, akkor A∪B is teljesíti azokat. Tegyük hát fel, hogy A és B ilyen kompakt halmazok, és írjuk fel rájuk vonatkozó Mayer-Vietoris sorozat (21.5. Tétel) egy darabkáját:
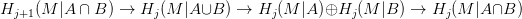
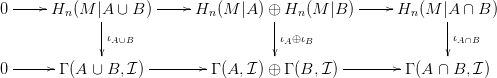
 és egy
B →
és egy
B →  szelés pontosan akkor áll össze egy A ∪ B →
szelés pontosan akkor áll össze egy A ∪ B →  szeléssé, ha
az A ∩ B felett a különbségük nulla. A két jobboldali függőleges nyíl
a feltétel miatt izomorfizmus, tehát az 5-lemma (2.9. Lemma) miatt
ιA∪B is izomorfizmus. Ezzel igazoltuk a redukciós lépést.
szeléssé, ha
az A ∩ B felett a különbségük nulla. A két jobboldali függőleges nyíl
a feltétel miatt izomorfizmus, tehát az 5-lemma (2.9. Lemma) miatt
ιA∪B is izomorfizmus. Ezzel igazoltuk a redukciós lépést.
Nevezzük tömör golyónak az olyan A ⊂ M részhalmazokat, amelyek
tömör golyók egy ℝn-nel homeomorf nyílt halmazban. Ha A egy
tömör golyó, akkor pontrahúzható, ezért  triviális nyaláb A fölött,
és így Γ(A,
triviális nyaláb A fölött,
és így Γ(A, )
) ℤ. Másrészt az (M|A) pár az (M|x) pár deformációs
retraktuma, ahol x ∈ M tetszőleges pont, ezért a Hn(M|A) →
Hn(M|x) megszorítás izomorfizmus minden x ∈ A pontban, és így
ιA izomorfizmus. A redukciós lépést többször egymás után alkalmazva
láthatjuk, hogy a a lemma teljesül minden olyan kompakt halmazra,
amelyik véges sok tömör golyó uniója.
ℤ. Másrészt az (M|A) pár az (M|x) pár deformációs
retraktuma, ahol x ∈ M tetszőleges pont, ezért a Hn(M|A) →
Hn(M|x) megszorítás izomorfizmus minden x ∈ A pontban, és így
ιA izomorfizmus. A redukciós lépést többször egymás után alkalmazva
láthatjuk, hogy a a lemma teljesül minden olyan kompakt halmazra,
amelyik véges sok tömör golyó uniója.
Legyen most A tetszőleges kompakt halmaz, tekintsünk egy olyan z ∈ Δi(M) láncot, melyre ∂z ∈ Δi−1(M \ A), azaz ∂z elkerüli az A halmazt. Legyen K ⊂ M egy olyan halmaz, ami tömör gömbök uniója, lefedi az A halmazt, de diszjunkt ∂z-től. Jelölje [z]A ∈ Hi(M|A) illetve [z]K ∈ Hi(M|K) a z által reprezentált homológia osztályt! Világos, hogy a Hi(M|K) → Hi(M|A) megszorítás a [z]K osztályt a [z]A osztályba viszi. tehát [z]K = 0 esetén [z]A is nulla.
Alkalmazzuk ezt az észrevételt az i > n esetre. Ekkor Hi(M|K) = 0, tehát [z]K = 0, és ezért [z]A = 0. Ez minden z relatív ciklusra igaz, tehát Hi(M|A) = 0.
Legyen most i = n, és tegyük fel, hogy [z]A képe nulla Γ(A, )-ben.
Ekkor [z]K képe is nulla Γ(K,
)-ben.
Ekkor [z]K képe is nulla Γ(K, )-ben. De Hn(M|K) → Γ(K,
)-ben. De Hn(M|K) → Γ(K, )
injektív, ezért [z]K = 0, és így [c]A = 0. Ez bizonyítja, hogy
Hn(M|A) → Γ(A,
)
injektív, ezért [z]K = 0, és így [c]A = 0. Ez bizonyítja, hogy
Hn(M|A) → Γ(A, ) is injektív.
) is injektív.
Végezetül tekintsünk egy σA ∈ Γ(A, ) szelést. Ez folytonosan
kiterjeszthető az A halmaz egy nyílt környezetére. Ezért van olyan
K halmaz és olyan σK ∈ Γ(K,
) szelést. Ez folytonosan
kiterjeszthető az A halmaz egy nyílt környezetére. Ezért van olyan
K halmaz és olyan σK ∈ Γ(K, ) szelés, melyre K véges sok tömör
gömb uniója, A ⊂ K, és σK megszorítása A-ra éppen σA. Mivel
K-ra igaz a lemma, azért van olyan ck ∈ Hn(M|K) osztály, melynek
képe Γ(K,
) szelés, melyre K véges sok tömör
gömb uniója, A ⊂ K, és σK megszorítása A-ra éppen σA. Mivel
K-ra igaz a lemma, azért van olyan ck ∈ Hn(M|K) osztály, melynek
képe Γ(K, )-ben éppen σK. Legyen cA ∈ Hn(M|A) a cK osztály
megszorítása. Világos, hogy CA képe Γ(A,
)-ben éppen σK. Legyen cA ∈ Hn(M|A) a cK osztály
megszorítása. Világos, hogy CA képe Γ(A, )-ben éppen σA. Ezért
Hn(M|A) → Γ(A,
)-ben éppen σA. Ezért
Hn(M|A) → Γ(A, ) szürjektív. □
) szürjektív. □
29.11. Definíció (Fundamentális osztály). Legyen
M egy n-dimenziós topológikus sokaság,  az irányítás nyalábja. Az M
irányítása egy olyam M →
az irányítás nyalábja. Az M
irányítása egy olyam M → folytonos szelés, amelyik minden x ∈ M
ponthoz az
folytonos szelés, amelyik minden x ∈ M
ponthoz az  x
x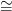 ℤ rost egyik generátorát rendeli. M irányítható, ha
van irányítása. A 29.10. Lemma miatt egy irányítás megadható egy
fundamentális osztállyal, azaz homológia-osztályok egy
ℤ rost egyik generátorát rendeli. M irányítható, ha
van irányítása. A 29.10. Lemma miatt egy irányítás megadható egy
fundamentális osztállyal, azaz homológia-osztályok egy
![{ }
[M ] = σK ∈ Hn (M |K; ℤ )](algebrai-topologia549x.png)
![[M ] = {σK } ∈ Klim⊆M Hn(M |K; ℤ )
kompakt](algebrai-topologia550x.png)
![[M ] ∈ Hn (M ;ℤ)](algebrai-topologia551x.png)
29.12. Tétel (Poincaré dualitás nyílt sokaságokra). Legyen M egy irányítható sokaság, [M] egy fundamentális osztálya. Az [M]-mel való sapka-szorzás izomorfizmus minden dimenzióban:
![D : Hk (M ;ℤ) −∼=→ H (M ;ℤ), D (x) = x ∩ [M ]
[M ] c n−k [M]](algebrai-topologia552x.png)
Bizonyítás. Hibás bizonyítás! Javítani kell!
Ebben a bizonyításban egész együtthatós homológiát és kohomológiát
használunk, elhagyjuk a ℤ-t a jelölésből. Minden A ⊆ M kompakt
halmazra jelölje σA ∈ Hn(M|A) az [M] képét (29.11. Definíció). Vegyük
észre, hogy a Kivágási Tétel (21.1. Tétel) miatt tetszőleges A ⊆ U nyílt
környezet esetén Hn(M|A) Hn(U,A), tekinthetünk σA-ra úgy, mint a
Hn(U|A) elemére. Most keresünk olyan U ⊆ M nyílt halmazokat,
melyeknek minden kompakt részhalmaza lefedhető olyan A ⊆ M kompakt
halmazzal, melyre a σA-val való sapka-szorzás izomorfizmus minden
dimenzióban:
Hn(U,A), tekinthetünk σA-ra úgy, mint a
Hn(U|A) elemére. Most keresünk olyan U ⊆ M nyílt halmazokat,
melyeknek minden kompakt részhalmaza lefedhető olyan A ⊆ M kompakt
halmazzal, melyre a σA-val való sapka-szorzás izomorfizmus minden
dimenzióban:
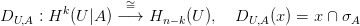 | (9) |
Ha egy U ⊆ M nyílt halmaz homeomorf ℝn-nel, akkor minden kompakt részhalmaza lefedhető egy A ⊆ U konvex kompakt részhalmazzal, és (9) következik a 29.5. Lemmából. Minden kompakt részhalmaz lefedhető véges sok ℝn-nel homeomorf nyílt halmazzal, tehát elegendő belátnunk a következő redukciót:
Hibás bizonyítás! Javítani kell!
ha (9) teljesül az A, B és A ∩ B halmazokra, akkor teljesül A ∪ B-re is. Az alábbi diagram felső sorában az M|A ∪ B = (M|A) ∪ (M|B) fedéshez tartozó Mayer-Vietoris sorozat látható (legalábbis annyi, amennyi odafért belőle), az alsó sorba pedig az M = M ∪M fedéshez tartozó Mayer-Vietoris sorozatot írtuk. δ∗ és ∂ ∗ jelölik a határ-homomorfizmusokat, a függőleges nyilak pedig a (9)-ban szereplő sapka szorzások:
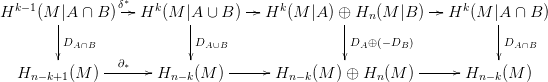
29.13. Tétel (Poincaré dualitás peremes sokaságokra). Legyen M egy n-dimenziós irányítható kompakt peremes sokaság, [M] ∈ Hn(M,∂M; ℤ) a fundamentális osztálya. Bontsuk fel a peremét két zárt részhalmazra: ∂M = A∪B, úgy, hogy A és B maguk is (n−1)-dimenziós peremes sokaságok, közös peremmel. Az [M]-mel való sapka-szorzás izomorfizmus minden dimenzióban:
![∼=
D[M ] : Hk (M, A; ℤ) −→ Hn −k(M, B; ℤ ), D [M ](x ) = x ∩ [M ]](algebrai-topologia556x.png)