31.1. Példa (komplex projektív tér). Az n-dimenziós komplex
projekív tér, ℂℙn, ideális hipersíkja ℂℙn−1, a „véges része” pedig ℂn.
Ez indukcióval megad egy olyan CW-felbontást, melyben összesen n + 1
cella van: 0-tól 2n-ig minden páros dimenzióban egy-egy. Ezért a ℂℙn
CW-lánc-komplexusának −1 fokszámtól 2n + 1 fokszámig terjedő része:
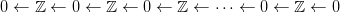 Minden páratlan fokszámon 0 áll. A homológia-csoportok:
Minden páratlan fokszámon 0 áll. A homológia-csoportok:
A kohomológia-csoportok:
A kohomológia-gyűrű egy „levágott polinom-gyűrű”, másodfokú generátorral.
A generátort első Chern-osztálynak hívjuk, jele c1.
![∕
H ∗(ℂ ℙn;ℤ ) = ℤ[c1] (cn1+1), deg (c1) = 2.](algebrai-topologia574x.png) Láttuk, hogy ℂℙn−1 egy hipersík ℂℙn-ben. Így a véges-dimenziós
projektív tereket egymásba ágyaztuk, uniójuk a
Láttuk, hogy ℂℙn−1 egy hipersík ℂℙn-ben. Így a véges-dimenziós
projektív tereket egymásba ágyaztuk, uniójuk a végtelen projektív tér
,
ℂℙ∞:
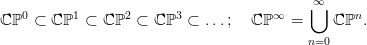
![H ∗(ℂℙ ∞;ℤ ) = ℤ[c1], deg(c1) = 2.](algebrai-topologia576x.png)
Ötlet. Legyen (x0,x1,…xk) egy homogén koordináta-rendszer a ℂℙk
téren! Jelölje Ai illetve Bi azt a két lineáris alteret ℂℙk-ben, amelyet
az xi+1 = xi+2 =  = xk = 0, illetve az x0 = x1 =
= xk = 0, illetve az x0 = x1 =  = xi = 0
egyenlet-rendszer határoz meg! Világos, hogy dim(Ai) = i és dim(Bi) =
k − i − 1, a két altér diszjunkt, és együtt kifeszítik az egyész ℂℙk
teret. Legyen
= xi = 0
egyenlet-rendszer határoz meg! Világos, hogy dim(Ai) = i és dim(Bi) =
k − i − 1, a két altér diszjunkt, és együtt kifeszítik az egyész ℂℙk
teret. Legyen  i azon komplex egyenesek halmaza, amelyek az Ai és
a Bi alterek egy-egy pontját kötik össze! Lásd be, hogy az Ai ∪ Bi
halmaz komplementumának minden pontján keresztül pontosan egy
i azon komplex egyenesek halmaza, amelyek az Ai és
a Bi alterek egy-egy pontját kötik össze! Lásd be, hogy az Ai ∪ Bi
halmaz komplementumának minden pontján keresztül pontosan egy
 i-beli egyenes halad át.
i-beli egyenes halad át.
Keress egy olyan ϕi : ℂℙk → ℂℙk transzformációt, amelyik
az Ai és a Bi altereket minden pontját helyben hagyja, az  i-beli
egyeneseket saját magukba képezi, az Ai altér egy Ui nyílt környezetét
homeomorfan képezi az Bi komplementumára, az Ui komplementumán
pedig egy retrakció a Bi altérre! (Tehát ϕi az Ui környezetet az Ai
centrumból az
i-beli
egyeneseket saját magukba képezi, az Ai altér egy Ui nyílt környezetét
homeomorfan képezi az Bi komplementumára, az Ui komplementumán
pedig egy retrakció a Bi altérre! (Tehát ϕi az Ui környezetet az Ai
centrumból az  i-beli egyenesek mentén „felfújja”, hogy kitöltse az
egész ℂℙk \ B
i halmazt.)
i-beli egyenesek mentén „felfújja”, hogy kitöltse az
egész ℂℙk \ B
i halmazt.)
Ezután keress olyan ψi : ℂℙk → ℂℙk transzformációt, amelyik
az Ai és az Bi altereket minden pontját helyben hagyja, az  i-beli
egyeneseket saját magukba képezi, az Ui zárt halmazon retrakció
az Ai altérre, az Ui komplementumát pedig homeomorfan képezi az
Ai komplementumára. (Tehát ψi az Ui komplementumát, ami az Ai
altér egy környezete, az Ai centrumból az
i-beli
egyeneseket saját magukba képezi, az Ui zárt halmazon retrakció
az Ai altérre, az Ui komplementumát pedig homeomorfan képezi az
Ai komplementumára. (Tehát ψi az Ui komplementumát, ami az Ai
altér egy környezete, az Ai centrumból az  i-beli egyenesek mentén
„felfújja”, hogy kitöltse az egész ℂℙk \ A
i halmazt.)
i-beli egyenesek mentén
„felfújja”, hogy kitöltse az egész ℂℙk \ A
i halmazt.)
Jelölje Δ az X = ℂℙk × ℂℙk szorzat-tér átlóját! Tekintsük a Φ
i =
ϕi × ψi szorzat-leképezéseket: ezek az X teret saját magára képezik.
Lásd be, hogy mindegyik Φi homotóp az identitás-leképezéssel!
Lásd be, hogy Φ0 úgy képezi a Δ sokaságot X-be, hogy az A0 × A0
pont egy környezetével irányítástartóan, egyrétegűen lefedi a ℂℙk ×
A0 részsokaságot, a környezet komplementumát pedig a B0 × ℂℙk
részsokaságba képezi!
Lásd be, hogy a Φ1∘Φ0 kompozíció úgy képezi a Δ sokaságot X-be,
hogy az (A1 × A1) ∩ Δ egyenes egy környezetével irányítástartóan,
egyrétegűen lefedi a ℂℙk×A
0 és a B0×A1 részsokaságokat, a környezet
komplementumát pedig a B1 × ℂℙk részsokaságba képezi!
Lásd be i szerinti teljes indukcióval, hogy a Φi ∘ Φi−1 ∘ ∘ Φ1 ∘ Φ0
kompozíció úgy képezi a Δ sokaságot X-be, hogy az (Ai × Ai) ∩ Δ
i-dimenziós altér egy környezetével irányítástartóan, egyrétegűen
lefedi a ℂℙk × A
0, B0 × A1, B1 × A2, ..., Bi−1 × Ai+1 részsokaságokat,
a környezet komplementumát pedig a Bi × ℂℙk részsokaságba képezi!
∘ Φ1 ∘ Φ0
kompozíció úgy képezi a Δ sokaságot X-be, hogy az (Ai × Ai) ∩ Δ
i-dimenziós altér egy környezetével irányítástartóan, egyrétegűen
lefedi a ℂℙk × A
0, B0 × A1, B1 × A2, ..., Bi−1 × Ai+1 részsokaságokat,
a környezet komplementumát pedig a Bi × ℂℙk részsokaságba képezi!
Tehát a Φk∘Φk−1∘ ∘Φ1∘Φ0 kompozíció úgy képezi a Δ sokaságot
X-be, hogy a kép irányítástartóan, egyrétegűen lefedi a ℂℙk × A
0,
B0 ×A1, B1 ×A2, ..., Bk−1 ×Ak részsokaságokat. Ebből már következik
az állítás. □
∘Φ1∘Φ0 kompozíció úgy képezi a Δ sokaságot
X-be, hogy a kép irányítástartóan, egyrétegűen lefedi a ℂℙk × A
0,
B0 ×A1, B1 ×A2, ..., Bk−1 ×Ak részsokaságokat. Ebből már következik
az állítás. □
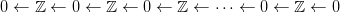
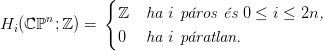
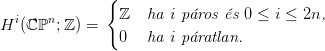
![∕
H ∗(ℂ ℙn;ℤ ) = ℤ[c1] (cn1+1), deg (c1) = 2.](algebrai-topologia574x.png)
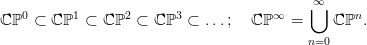
![H ∗(ℂℙ ∞;ℤ ) = ℤ[c1], deg(c1) = 2.](algebrai-topologia576x.png)
![∗( ∞ ∞ ) ∼
H ℂ ℙ × ℂℙ ;ℤ = ℤ[x,y ]; deg (x) = deg(y) = 2](algebrai-topologia577x.png)
; deg(x) = deg(y) = 2](algebrai-topologia578x.png)
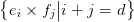
![( ) {
xpyq [ei × f j] = 1 ha i = p és j = q,
0 különben.](algebrai-topologia580x.png)
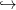
![{
∑ ∗ i j ci ha i = j,
δ∗[ck] = [ei × fj] és δ x y = 0 k ülönben.
i+j=k](algebrai-topologia582x.png)





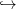
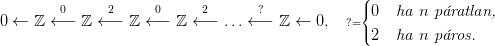
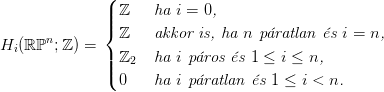
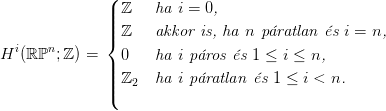
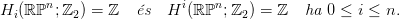
![∕
H ∗(ℝ ℙn;ℤ ) = ℤ [w ] (wn+1), deg(w ) = 1.
2 2 1 1 1](algebrai-topologia592x.png)
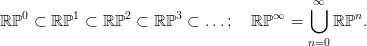
![H ∗(ℝ ℙ∞; ℤ2) = ℤ2 [w1 ], deg(w1) = 1.](algebrai-topologia594x.png)