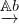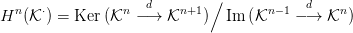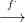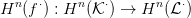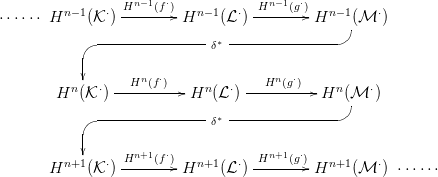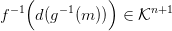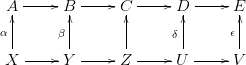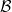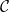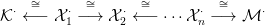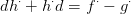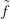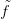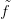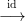2. Komplexusok
2.2. Definíció. Ebben a jegyzetben Ab jelöli az Abel csoportok
kategóriáját, és 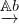 jelöli az Abel csoport komplexusok kategóriáját.
jelöli az Abel csoport komplexusok kategóriáját.
2.4. Konvenció. Ha az 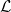 ⋅ komplexust alul indexeljük, akkor a
homológia-modulusait is alsó indexszel írjuk: Hn(
⋅ komplexust alul indexeljük, akkor a
homológia-modulusait is alsó indexszel írjuk: Hn(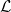 ⋅).
⋅).
2.5. Feladat. Bizonyítsd be, hogy a 2.3. Definícióban f(k) valóban
reprezentál egy homológia-osztályt (azaz d f(k)
f(k)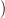 = 0), és ez az
osztály nem függ k-tól, csak a homológia-osztályától, k-tól. Bizonyítsd
be, hogy Hn tényleg funktor: kompatibilis a lánc-homomorfizmusok
kompozíciójával.
= 0), és ez az
osztály nem függ k-tól, csak a homológia-osztályától, k-tól. Bizonyítsd
be, hogy Hn tényleg funktor: kompatibilis a lánc-homomorfizmusok
kompozíciójával.
2.7. Feladat. Diagram vadászat! Lásd be, hogy a 2.6. Tételben a
formula valóban egy homológia-osztályt reprezentál, és a kapott δ∗m
osztály nem függ a választásoktól.
2.8. Feladat. Diagram vadászat! Lásd be, hogy a 2.6. Tételben
szereplő sorozat valóban egzakt.
2.9. Lemma (5-lemma). Tegyük fel, hogy az alábbi diagram (előjel
erejéig) kommatív, a sorai egzaktak, és a görög betűvel jelölt függőleges
nyilak mind izomorfizmusok. Ekkor az ötödik (betű nélküli) függőleges
nyíl is izomorfizmus.
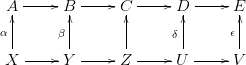
2.10. Feladat. Diagram vadászat! Lásd be a 2.9. Lemmát!
Ötlet: Következik a 2.6. Tételből. Másik lehetőség: egyszerű diagram
vadászat. □
2.13. Megjegyzés. A 2.12. Definícióban elegendő lenne két lépéses
láncolatokat használni (azaz n = 1). Ha a komplexusok kategóriáját
úgy módosítjuk, hogy a lánc-ekvivalenciákat izomorfizmusokká tesszük
(tehát bevezetjük az inverzüket, és az azokból kiszámítható összes
kompozíciót is), akkor a modulus-kategória derivált kategóriájához
jutunk.
2.15. Tétel. Ha f⋅,g⋅ :  ⋅ →
⋅ → 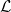 ⋅
lánc-homotóp lánc-homomorfizmusok, akkor Hn(f⋅) = Hn(g⋅) minden
n-re. Ha f homotóp ekvivalencia, akkor lánc-ekvivalencia.
⋅
lánc-homotóp lánc-homomorfizmusok, akkor Hn(f⋅) = Hn(g⋅) minden
n-re. Ha f homotóp ekvivalencia, akkor lánc-ekvivalencia.
2.16. Feladat. Bizonyítsd be a 2.15. Tételt.
2.18. Feladat. Lásd be a 2.17. Következményt közvetlenül, diagram
vadászattal.
2.19. Megjegyzés. A 2.15. Tétel támasztja alá azt a filozófiát, hogy
egy komplexust bármikor kicserélhetünk egy vele lánc-ekvivalensre.
Speciális eset: egy modulus helyett dolgozhatunk egy projektív vagy egy
injektív feloldásával (lásd a 4.2. Definíciót és a 4.3. Definíciót).
 ⋅ komplexus az alábbi, R-modulusokból álló
(mindkét irányban végtelen) diagramot jelöli:
⋅ komplexus az alábbi, R-modulusokból álló
(mindkét irányban végtelen) diagramot jelöli:
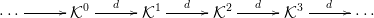
 ⋅ komplexus
felülről korlátos, ha egy p0 indextől kezdve minden p > p0 indexre
⋅ komplexus
felülről korlátos, ha egy p0 indextől kezdve minden p > p0 indexre
 p = 0, és alulról korlátos, ha egy n
0 indextől kezdve minden n < n0
indexre
p = 0, és alulról korlátos, ha egy n
0 indextől kezdve minden n < n0
indexre  p = 0. Azt mondjuk, hogy
p = 0. Azt mondjuk, hogy  ⋅ valamerről kotlátos, ha a két
korlátossági feltétel közül az egyik teljesül.
⋅ valamerről kotlátos, ha a két
korlátossági feltétel közül az egyik teljesül.
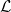 ⋅ egy másik komplexus. Egy f⋅ :
⋅ egy másik komplexus. Egy f⋅ :  ⋅ →
⋅ →  ⋅
lánc-homomorfizmus a következő kommutatív diagramot jelöli:
⋅
lánc-homomorfizmus a következő kommutatív diagramot jelöli:
 ⋅
⋅
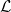 ⋅
⋅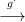
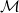 ⋅ sorozata egzakt, ha a
benne szereplő
⋅ sorozata egzakt, ha a
benne szereplő  n
n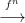
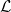 n
n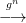
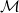 n sorozatok mind egzaktak.
n sorozatok mind egzaktak.