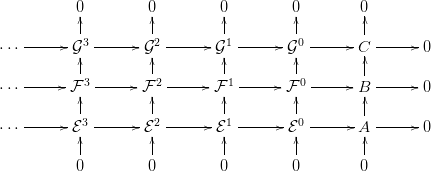
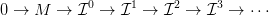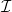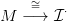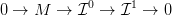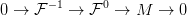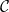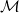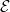4. Projektív, injektív, lapos feloldások
4.1. Definíció. Egy M modulus projektív, ha a Hom(M, ) funktor
egzakt. Azt mondjuk, hogy M injektív, ha a Hom( ,M) funktor egzakt.
És végül M lapos, ha a ⊗ M funktor egzakt.
4.4. Tények.
-
(a)
- Minden szabad modulus projektív, minden projektív modulus
lapos.
-
(b)
- Minden modulusnak van szabad feloldása (tehát projektív és lapos
feloldása is).
-
(c)
- Egy modulus pontosan akkor projektív, ha egy szabad modulus
direkt összeadandója.
-
(d)
- Minden injektív modulus osztható.
-
(e)
- Minden modulusnak van injektív burka, azaz van egy őt
tartalmazó legkisebb injektív modulus. Ezért minden modulusnak
van injektív feloldása.
-
(f)
- Nullosztómentes főideálgyűrű felett lapos = torziómentes.
-
(g)
- Nullosztómentes főideálgyűrű felett injektív = osztható. Ezért
ilyenkor egy injektív modulus faktormodulusa injektív.
-
(h)
- Nullosztómentes főideálgyűrű felett egy szabad modulus minden
részmodulusa szabad. Ezért ilyenkor projektív = szabad.
-
(i)
- Nullosztómentes főideálgyűrű felett minden modulusnak van
kétlépéses injektív feloldása:
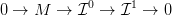 és kétlépéses szabad feloldása:
és kétlépéses szabad feloldása:
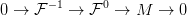 (Azonnal következik (g)-ből illetve (h)-ből.)
(Azonnal következik (g)-ből illetve (h)-ből.)
4.7. Feladat. Diagram vadászat! Dolgozd ki a 4.6. Lemma
bizonyítását!
4.8. Definíció. Noether gyűrű feletti modulusok egy  ⋅ komplexusa
véges típusú, ha minden homológiája végesen generált, és Hn(
⋅ komplexusa
véges típusú, ha minden homológiája végesen generált, és Hn( ⋅) = 0,
ha n < n0 (valamilyen n0 értékre).
⋅) = 0,
ha n < n0 (valamilyen n0 értékre).
4.10. Feladat. Diagram vadászat! Bizonyítsd be a 4.9. Lemma!
4.11. Feladat. Van-e analógja a 4.9. Lemmanak injektív
modulusokkal?
4.12. Feladat. Lásd be, hogy projektív modulusok tenzor szorzata
ismét projektív, valamint lapos modulusok tenzor szorzata ismét lapos!
Mi a helyzet injektív modulusok, illetve szabad modulusok tenzor
szorzatával?
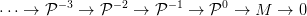
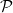 n modulus projektív. Ha az M helyére is nullát írunk,
a kapott
n modulus projektív. Ha az M helyére is nullát írunk,
a kapott 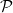 ⋅ komplexus az M egy projektív feloldása. Érdemes most
úgy gondolni az M modulusra, mint egy olyan komplexusra, amelynek a
0-fokú része M, minden más fokszámon pedig 0 áll. Ekkor tehát a fenti
egzakt sorozat azt jelenti, hogy a
⋅ komplexus az M egy projektív feloldása. Érdemes most
úgy gondolni az M modulusra, mint egy olyan komplexusra, amelynek a
0-fokú része M, minden más fokszámon pedig 0 áll. Ekkor tehát a fenti
egzakt sorozat azt jelenti, hogy a
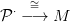
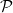 n
modulusok nem csak projektívek, hanem még szabadok is, akkor
n
modulusok nem csak projektívek, hanem még szabadok is, akkor 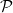 ⋅ egy
szabad feloldás. Sokszor a projektivitás helyett elég csak azt megkövetelni,
hogy a
⋅ egy
szabad feloldás. Sokszor a projektivitás helyett elég csak azt megkövetelni,
hogy a 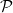 n modulusok laposak legyenek — ilyenkor lapos feloldásról
beszélünk.
n modulusok laposak legyenek — ilyenkor lapos feloldásról
beszélünk.