3. Kettős komplexusok
3.5. Feladat. Lásd be, hogy a 3.4. Definícióban szereplő q + s kitevő
helyes, azaz
![-------⋅+s
K [s]⋅ = K [s,s] .](algebrai-topologia30x.png)
3.9. Konvenció. Gyakran szükség van arra, hogy egy kettős
komplexust blokkokból építsünk fel. Az alábbi sematikus diagramok ilyen
kettős komplexusokat mutatnak. Itt most  ⋅,
⋅, 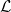 ⋅ komplexusok,
⋅ komplexusok, 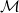 ⋅⋅ pedig
egy kettős komplexus, és a diagramon kívüli területekre nullákat kell
írni:
⋅⋅ pedig
egy kettős komplexus, és a diagramon kívüli területekre nullákat kell
írni:
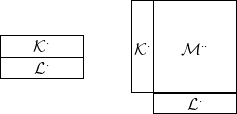 Figyeljük meg, hogy egy komplexust vízszintesen és függőlegesen is
beépíthetünk egy kettős komplexusba. Természetesen, ha a diagramba
írt komplexusok valamelyik irányban végtelenek, akkor a belőlük épített
diagram is végelen lesz abban az irányban (noha a diagramon erre
semmi nem utal). Az ilyen diagramokon nem tudjuk jelölni az egyes
blokkok közt haladó differenciálokat, ezért csak olyan helyzetekben használjuk
őket, amikor egyértelmű, hogy melyik homomorfizmusokról van szó.
Figyeljük meg, hogy egy komplexust vízszintesen és függőlegesen is
beépíthetünk egy kettős komplexusba. Természetesen, ha a diagramba
írt komplexusok valamelyik irányban végtelenek, akkor a belőlük épített
diagram is végelen lesz abban az irányban (noha a diagramon erre
semmi nem utal). Az ilyen diagramokon nem tudjuk jelölni az egyes
blokkok közt haladó differenciálokat, ezért csak olyan helyzetekben használjuk
őket, amikor egyértelmű, hogy melyik homomorfizmusokról van szó.
3.11. Feladat. Ellenőrizd, hogy a 3.10. Definícióban helyesen írtuk
fel az egzakt sorozatot.
3.13. Lemma. A 3.10. Definícióhoz tartozó hosszú egzakt sorozat
(lásd a 2.6. Tételben) így néz ki:
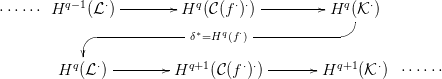
3.14. Feladat. Diagram vadászat! Ellenőrizd, hogy a
3.13. Lemma diagramján látható indexek helyesek! Lásd be, hogy a δ∗
határ-homomorfizmus valóban megegyezik Hq(f⋅)-fel!
3.15. Lemma. Egy lánc-ekvivalencia leképezés-kúpja egzakt.
Ötlet: Ez a lemmát bebizonyítható egyszerű diagram vadászattal. Egy
másik lehetőség, hogy megmutatjuk: a leképezés-kúp pontra húzható
(lásd a 2.17. Következményt). A
 ⋅ ⋅ |
 ⋅ ⋅ |
kettős komplexusban a függőleges
(identitás)homomorfizmus inverzéből könnyedén elkészíthetjük a
kívánt lánc-homotópiát. Harmadik módszer: azonnal következik
az állítás abból az észrevételből, hogy a
3.13. Lemma egzakt
sorozatában a
δ∗ határ-homomorfizmusok mind izomorfizmusok.
□
3.16. Feladat. Dolgozd ki a 3.15. Lemma bizonyításához adott
ötleteket.
3.17. Feladat. Lásd be, hogy egy lánc-homomorfizmus pontosan akkor
lánc-ekvivalencia, ha leképezés-kúpja egzakt.
Ötlet: Használd a 3.13. Lemma hosszú egzakt sorozatát. □
3.19. Megjegyzés. Érdemes összevetni a leképezés-kúpról szóló
feladatokat a triangulált kategória fogalámával.
3.21. Feladat. Diagram vadászat! Lásd be a 3.20. Tételt!
3.23. Feladat. Miért van a ⋅ + (s + 1) index-eltolás a
3.22. Következményben?
Bizonyítás. Alkalmazzuk a 3.22. Következményt illetve a 45-fokos
egyenesre tükrözött változatát a következő komplexusokra:
 □
□
Bizonyítás. A  ⋅⋅ totális komplexusa (lásd a 3.3. Definíciót) éppen
a ∂⋅ :
⋅⋅ totális komplexusa (lásd a 3.3. Definíciót) éppen
a ∂⋅ :  [p]⋅ →
[p]⋅ →  [p + 1]⋅ lánc-homomorfizmus (a függőleges irányú
differenciál) leképezés-kúpja (lása a 3.10. Definíciót). Írjuk fel a
3.13. Lemma egzakt sorozatának egy darabját:
[p + 1]⋅ lánc-homomorfizmus (a függőleges irányú
differenciál) leképezés-kúpja (lása a 3.10. Definíciót). Írjuk fel a
3.13. Lemma egzakt sorozatának egy darabját:
![-- Hq(∂⋅) --
Hp+q (K ⋅) -----Hq (K[p]⋅) -----------Hq (K [p + 1]⋅) -----Hp+q+1 (K ⋅)
|| ||
|| ||
p,q p+1,q
0 ------------E1 ----------------- E1 --------------0](algebrai-topologia51x.png)
A diagram alsó sora éppen az
E1⋅⋅ táblázat
q-adik oszlopa. Leolvasható
róla, hogy
minden
q-ra. A Tétel most már kiolvasható a fenti egzakt sorozat egy
másik darabjából:
![q−1 ⋅ -- q ⋅
--H---(∂)--Hq −1(K [p + 1 ]⋅)---- Hp+q (K ⋅)-----Hq (K [p]⋅)---H-(∂-)--](algebrai-topologia53x.png) □
□
3.27. Feladat. Tekintsük a 3.26. Tételbeli  ⋅⋅ komplexust, jelölje D⋅ a
⋅⋅ komplexust, jelölje D⋅ a  ⋅
(totális) komplexus differenciálját. Kövesd a 3.26. Tétel bizonyítását az
alábbi explicit formulákkal!
⋅
(totális) komplexus differenciálját. Kövesd a 3.26. Tétel bizonyítását az
alábbi explicit formulákkal!
-
(a)
- Lásd be, hogy
-
(b)
- Tekintsük a következő részmodulust:
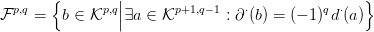 Az alábbi képletekben kivételesen kiírjuk a d⋅ differenciál indexét.
A 3.26. Tétel bizonyítása alapján lásd be, hogy
Az alábbi képletekben kivételesen kiírjuk a d⋅ differenciál indexét.
A 3.26. Tétel bizonyítása alapján lásd be, hogy
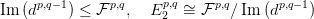
-
(c)
- Az eddigiekből következik,
hogy Hp+q

 ⋅
⋅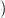 elemei reprezentálhatók Ker(Dp+q) elemeivel, és
E2p,q elemei reprezentálhatók
elemei reprezentálhatók Ker(Dp+q) elemeivel, és
E2p,q elemei reprezentálhatók 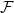 p,q elemeivel. Lásd be, hogy a
3.26. Tételbeli Hp+q
p,q elemeivel. Lásd be, hogy a
3.26. Tételbeli Hp+q
 ⋅
⋅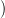 → E
2p,q homomorfizmus megadható a
következő módon:
→ E
2p,q homomorfizmus megadható a
következő módon:
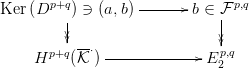
-
(d)
- Most ismét kiírjuk a d⋅ differenciál indexét. Tekintsük a
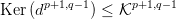 részmodulust. Lásd be, hogy E2p+1,q−1 ennek a hányados-modulusa!
Lásd be, hogy az a 3.26. Tételbeli E2p+1,q−1 → Hp+q
részmodulust. Lásd be, hogy E2p+1,q−1 ennek a hányados-modulusa!
Lásd be, hogy az a 3.26. Tételbeli E2p+1,q−1 → Hp+q
 ⋅
⋅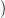 homomorfizmus
megadható a következő módon:
homomorfizmus
megadható a következő módon:
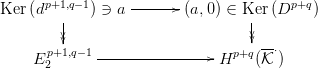
3.28. Tétel. Legyen R egy nullosztómentes főideálgyűrű. Tegyük fel,
hogy a 3.26. Tételbeli kettős komplexus R feletti szabad modulusokból
áll. Ekkor a 3.26. Tétel egzakt sorozata felhasad. (Ez a felhasítás nem
kanonikus.)
Bizonyítás. A bizonyításban felhasználjuk a 3.27. Feladatot.
Tekintsük a (c) pontban szereplő diagramot, az alábbi jelölésekkel:
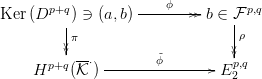
Mivel most
 p,q
p,q szabad modulus (
4.4. Tények (
h) pont), azért választhatunk
egy
homomorfizmust, ami
ϕ-nek jobboldali inverze (azaz
ϕ-vel komponálva
az
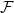 p,q
p,q identitás-izomorfizmusát adja). Mivel
ϕ szürjektív, azért
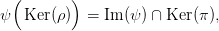
tehát
ψ indukál egy
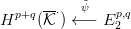
homomorfizmust, ami
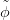
-nek jobboldali inverze.
□
 ⋅⋅ kettős komplexus az alábbi síkbeli
kommutatív diagram, amelynek minden sora és minden oszlopa
komplexus (azaz d∂ = ∂d, d2 = 0 és ∂2 = 0).
⋅⋅ kettős komplexus az alábbi síkbeli
kommutatív diagram, amelynek minden sora és minden oszlopa
komplexus (azaz d∂ = ∂d, d2 = 0 és ∂2 = 0).
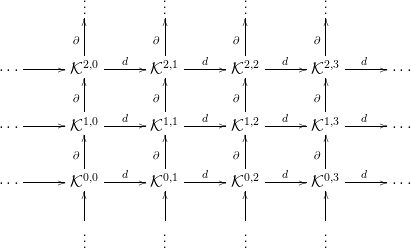
 ⋅⋅ kettős komplexus átlósan korlátos, ha minden n-re a
⋅⋅ kettős komplexus átlósan korlátos, ha minden n-re a  p,n−p
modulusok között csak véges sok nem-nulla szerepel.
p,n−p
modulusok között csak véges sok nem-nulla szerepel.
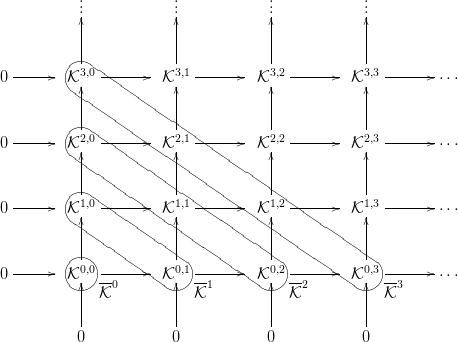 1. ábra. Totális komplexus
1. ábra. Totális komplexus
![{ p,q
K[s,t]p,q = K ha s ≤ p ≤ t , K [s]q = K-[s,s]q+s = Ks,q.
0 különben](algebrai-topologia29x.png)
![-------⋅+s
K [s]⋅ = K [s,s] .](algebrai-topologia30x.png)
![------⋅ ------⋅ ----------⋅
0 − → K[s,t] −→ K [r,t] −→ K [r,s − 1]− → 0](algebrai-topologia31x.png)
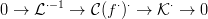 2. ábra. Kettős komplexus szeletei
2. ábra. Kettős komplexus szeletei
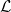
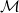

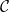
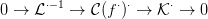
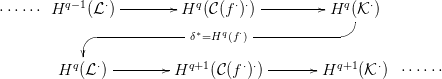

![|-----------------|- |------------------|
| | | K [s ]⋅ |
| | |------------------|
| K [s + 1,∞ ]⋅⋅ | | |
| | vagy | |
| | | K [− ∞, s − 1]⋅⋅ |
|----------⋅------|- | |
-------K[s]--------- --------------------](algebrai-topologia43x.png)
![------------⋅+(s+1) -------------⋅+(s+1)
K [s]⋅ ∼= K [s + 1,∞ ] illetve K [s]⋅ ∼= K [− ∞, s − 1 ] .](algebrai-topologia44x.png)
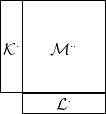


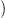
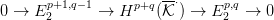

![-- Hq(∂⋅) --
Hp+q (K ⋅) -----Hq (K[p]⋅) -----------Hq (K [p + 1]⋅) -----Hp+q+1 (K ⋅)
|| ||
|| ||
p,q p+1,q
0 ------------E1 ----------------- E1 --------------0](algebrai-topologia51x.png)
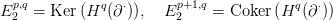
![q−1 ⋅ -- q ⋅
--H---(∂)--Hq −1(K [p + 1 ]⋅)---- Hp+q (K ⋅)-----Hq (K [p]⋅)---H-(∂-)--](algebrai-topologia53x.png)
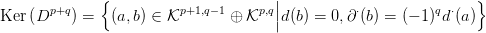
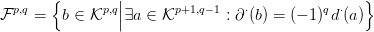
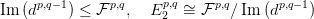

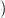
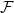

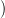
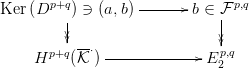
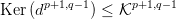

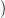
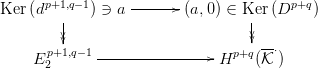
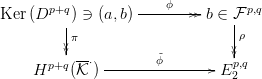
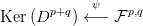
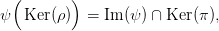
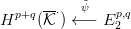
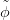 -nek jobboldali inverze.
-nek jobboldali inverze.