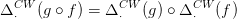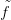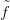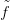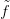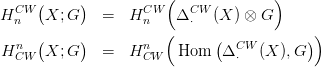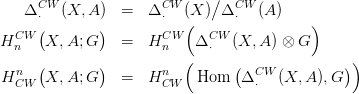15. CW-homológia, CW-kohomológia
Ebben a fejezetben sokat dolgozunk irányított sokaságokkal. Ez egy jól
ismert fogalom, ha a dimenzió legalább egy, de érdemes pár szót szólni a
nulla dimenziós sokaságokról:
15.1. Definíció. Egy 0-dimenziós sokaság irányítása azt jelenti,
hogy minden pontja kap egy előjelet (+ vagy −). Egy 1-dimenziós
irányított kompakt sokaság peremét úgy irányítjuk, hogy a benne
szereplő szakaszok végpontjai + előjelet kapnak, a kezdőpontok pedig −
előjelet.
Legyen X egy irányított kompakt 0-dimenziós sokaság, P egy
irányított pont, f pedig az X → {P} leképezés (csak egy ilyen
van). Jelölje deg(X) az X-beli + illetve − előjelű pontok számának
különbségét! Ha P előjele +, akkor deg(f) = deg(X), ha pedig P előjele
negatív, akkor deg(f) = − deg(X).
15.2. Konvenció. Ebben a fejezetben CW-komplexusokkal
dolgozunk. Az n-cellák — definíció szerint — azonosítva vannak az
n-dimenziós tömör egységgöbbbel, ezért irányított peremes sokaságok,
a 0-cellák mindig + előjelet kapnak. Az n-cellák pereme tehát irányított
(n−1)-dimenziós gömb. Speciálisan, az 1-cellák peremében a végpont +
elöjelet, a kezdőpont − előjelet kap.
15.3. Definíció. Legyen X egy CW-komplexus. Használjuk a
14.1. Konvenció jelöléseit! Minden n ≥ 0-ra legyen ΔnCW (X) az X
n-cellái által generált szabad Abel csoport. Amikor csoport-elemekről
beszélünk, [enα]-nel jelöljük az e
nα cellát. Legyen e
nα egy n-cella, e
n−1β
pedig egy (n − 1)-cella. Tekintsük az alábbi kompozíciót:
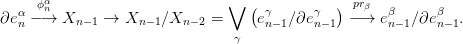 Ez egy
Ez egy
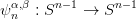 folytonos függvény. Könnyen látható, hogy minden enα cellához csak
véges sok olyan en−1β cella található, amelyre a deg(ψ
nα,β) fokszám (lásd
a 13.10. Definíció) nem nulla. Minden n-re definiálunk egy homomorfizmust:
folytonos függvény. Könnyen látható, hogy minden enα cellához csak
véges sok olyan en−1β cella található, amelyre a deg(ψ
nα,β) fokszám (lásd
a 13.10. Definíció) nem nulla. Minden n-re definiálunk egy homomorfizmust:
![∂ ( ) ∑
ΔCWn (X )− → ΔCWn− 1(X ) , ∂ [eαn] = deg(ψnα,β) ⋅ [eβn− 1].
β](algebrai-topologia271x.png) ΔnCW (X) elemeit n
ΔnCW (X) elemeit n-láncoknak
hívjuk. Ha L egy n-lánc, akkor ∂L-et
hívjuk az L határának
.
Be fogjuk látni, hogy a ΔnCW (X) csoportok
a fenti homomorfizmusokkal egy komplexust alkotnak. Ez a Δ⋅CW (X)
komplexus az X tér CW-lánc-komplexusa.
15.4. Feladat. Lásd be, hogy a 15.3. Definícióban minden enα
cellához csak véges sok olyan en−1β cella található, amelyre
deg(ψnα,β)≠0.
Ötlet: A kompaktság miatt csak véges sok olyan cella van, amelyik
teljes egészében benne van ϕnα képében. □
Az előző két definícióban a 13.10. Definíció segítségével konstruáltunk
láncokat. Ezt a konstrukciót szeretnénk most általánosítani. n-cellák
helyett azonban most egy tetszőleges n-dimenziós sokaságot képezünk
Xn-be.
15.7. Feladat. A 15.6. Definícióban az f leképezés az X n-vázába
érkezett. Miért nem engedhetünk meg minden folytonos f : M → X
leképezést, melyre f(∂M) ⊆ Xn−1?
15.8. Tétel. Legyen X egy CW-komplexus, M egy kompakt peremes
n-dimenziós differenciálható sokaság, és f : M → Xn egy folytonos függvény,
ami az M peremét Xn−1-be képezi. Ekkor
![( )
∂ f [M ] = f [∂M ],
∗ ∗](algebrai-topologia282x.png) | (3) |
ahol a bal oldalon a 15.3. Definíció ∂ homomorfizmusa szerepel, a
jobboldalon ∂M pedig az M pereme. Speciális esetben:
![( )
ha M zárt, akkor ∂ f∗[M ] = 0.](algebrai-topologia283x.png)
Bizonyítás. A 13.11. Tétel szerint az egyenlet két oldala nem változik,
ha az f-et kicseréljük egy vele homotóp leképezésre. Öt lépésben fogjuk
az f-et feljavítani. Legyen enγ ⊆ X egy olyan n-cella, amelyik teljes
egészében benne van az f(M) képhalmazban. Az első két lépésben
olyan homotópiákat alkalmazunk az f-re, amelyek csak az f−1(e
nγ)
halmazon változtatják.
1. lépés. A 13.7. Tétel segítségével elérjük, hogy legyen olyan
Dγ n-dimenziós golyó az e
nγ cella belsejében, amelynek f−1(Dγ)
ősképe véges sok páronként diszjunkt n-dimenziós golyóból áll, és ezek
mindegyikét f homeomorfan képezi Dγ-ra.
2. lépés. Alkalmazunk még egy homotópiát, amelyik a Dγ golyókat
„felfújja”, hogy betöltse vele az egész enγ cellát, az e
nγ\Dγ héjat pedig
az enγ peremébe deformálja.
3.lépés. Az első két lépés deformációit megismételjük az összes olyan
n-cellára, amelyik teljes egészében benne van az f(M) képhalmazban.
4. lépés. Legyen enβ egy olyan n-cella, amelyik kimaradt a 3.
lépésben, tehát amelyiknek van f(M)-en kívül eső pontja. Egy
homotópiával ebből a pontból „kifújjuk” az enβ cella tartalmát a
peremre, tehát a homotópia alkalmazása után f(M) elkerüli enβ
belsejét.
5. lépés, A 4. lépést megismételjük az összes olyan enβ cellára,
amelyik nem szerepelt a 3. lépésben. Ezzel elérjük, hogy M belsejében
legyen véges sok páronként diszjunkt n-dimenziós golyó, B1,…Bm,
melyek mindegyikét f homeomorfan képezi valamelyik n-cellára, és a
komplementumot az X (n − 1)-vázába képezi.
Legyen B az összes Bi uniója. Ez egy peremes sokaság, és
világos, hogy az f megszorítása B-re minden egyes n-cellát pontosan
annyiszor fed le (előjelesen számolva), mint az illető cella együtthatója
f∗[M]-ben. Könnyen látható tehát, hogy
![( )
f∗[B ] = f∗[M ] és f∗[∂B ] = ∂ f ∗[M ] .](algebrai-topologia284x.png)
Legyen
N az a peremes sokaság, amit úgy kapunk, hogy
M-ből kivágjuk
a
B belsejét. Világos, hogy
f(N) ⊆ Xn−1, tehát
13.11. Tétel(
c) miatt
![f ∗[∂N ] = 0.](algebrai-topologia285x.png)
Az
N pereme, mint halmaz, az
M és a
B pereméből áll össze — de
B peremén meg kell fordítani az irányítást, hiszen
N és
B a perem
„szemközti oldalán” helyezkedik el. Ezért
![f∗[∂M ] − f∗[∂B ] = f∗[∂N ] = 0.](algebrai-topologia286x.png)
A fenti kiemelt egyenleteket összevetve kapjuk a (
3) egyenletet.
□
15.9. Tétel. Legyenek X, Y CW-komplexusok, f,g : X → Y
CW-függvények, és h : X × [0, 1|→ Y egy CW-homotópia f és g
között.
-
(a)
- Δ⋅CW (X) komplexus, azaz ∂2 = 0.
-
(b)
- f∗ : Δ⋅CW (X) → Δ
⋅CW (Y ) egy lánc-leképezés.
-
(c)
- h indukál egy lánc-homotópiát f∗ és g∗ között.
Bizonyítás. Használjuk a 14.1. Konvenció jelöléseit. Legyen enα az X
egyik n-cellája, Φ : enα → X pedig az a leképezés, amelyik a cella
belsejében az identitás, a peremen pedig megegyezik a ϕnα ragasztó
leképezéssel. Az enα cella egy peremes sokaság, és a 15.6. Definícióból
azonnal következik, hogy Φ∗ enα
enα![]](algebrai-topologia288x.png) éppen az
éppen az  e
nα
e
nα![]](algebrai-topologia290x.png) ∈ Δ
nCW (X)
generátor elem. A 15.8. Tétel miatt tehát ∂
∈ Δ
nCW (X)
generátor elem. A 15.8. Tétel miatt tehát ∂ enα
enα![]](algebrai-topologia292x.png) = Φ
∗
= Φ
∗ ∂enα
∂enα![]](algebrai-topologia294x.png) . Ha most
az ∂enα zárt sokaságra is alkalmazzuk a 15.8. Tételt, akkor azt kapjuk,
hogy ∂2
. Ha most
az ∂enα zárt sokaságra is alkalmazzuk a 15.8. Tételt, akkor azt kapjuk,
hogy ∂2 e
nα
e
nα![]](algebrai-topologia296x.png) = 0. Ez Δ
nCW (X) minden generátorára teljesül, amiből
következik az (a) állítás.
= 0. Ez Δ
nCW (X) minden generátorára teljesül, amiből
következik az (a) állítás.
A f∘Φ kompozítió az enα peremes sokáságot az Y CW-komplexusba
képezi. Összevetve a 15.6. Definíciót a 15.5. Definícióval láthatjuk,
hogy az f∗[enα] lánc megegyezik az (f ∘Φ)
∗[enα] lánccal. A 15.8. Tétel
miatt tehát ∂ f∗[enα]
f∗[enα]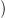 = (f ∘ Φ)
∗[∂enα], amiről az (a) pontban már
láttuk, hogy megegyezik az f∗
= (f ∘ Φ)
∗[∂enα], amiről az (a) pontban már
láttuk, hogy megegyezik az f∗ ∂[enα]
∂[enα]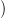 lánccal. Ezzel beláttuk a (b)
állítást.
lánccal. Ezzel beláttuk a (b)
állítást.
Végül a h homotópia segítségével definiálunk minden n-re egy
Lh : ΔnCW (X) → Δ
n+1CW (Y ) homomorfizmust:
![(
Ln [eαn]) = h∗[eαn × [0,1 ]].](algebrai-topologia301x.png)
Az
enα × [0, 1] határa három, a peremük mentén összeragasztott,
peremes sokaságból áll:
![( )
∂ eαn × [0,1] = ∂eαn × [0,1] ∪ en α × {0} ∪ enα × {1}.](algebrai-topologia302x.png)
Szigorúan véva
enα×[0, 1] nem peremes sokaság (éle van), de homeomorf
egy
B tömör golyóval, tehát alkalmazhatjuk rá a
15.8. Tételt. Mivel
h az „éleket” az
X (n − 1)-vázába viszi, azért jogos
h∗[∂B] összegre
bontása az aábbi egyenletben:
![( α [ α ]
∂Ln [en]) = ∂h∗ en × [0,1] = h∗[∂B ] =](algebrai-topologia303x.png)
![[ α ] [ ] [ ] ( )
= h ∗∂e n× [0,1 ]+h ∗ enα ×{0 } +h ∗ enα× {1} = Ln −1 ∂[en] +f ∗[en]− g∗[en]](algebrai-topologia304x.png)
Ebből látjuk, hogy az
Ln homomorfizmusok összeállnak egy
f∗ és
g∗
közti
Δ⋅CW (X) → Δ
⋅CW (Y ) lánc-homotópiává. Beláttuk a (
c) állítást
is.
□
15.11. Tétel.
-
(a)
- Δ⋅CW : Top CW →
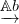 egy kovariáns funktor. (2.2. Definíció és
14.3. Definíció).
egy kovariáns funktor. (2.2. Definíció és
14.3. Definíció).
-
(b)
- Ha f,g homotóp CW-függvények (tetszőleges folytonosan
homotópiával), akkor Δ⋅CW (f) és Δ
⋅CW (g) lánc-homotópok.
-
(c)
- Ha h egy olyan CW-függvény, amelyik gyenge homotóp
ekvivalencia, akkor Δ⋅CW (h) egy lánc-ekvivalencia.
-
(d)
- Ha az X CW-komplexus pontrahúzható (topológikus térként),
akkor Δ⋅CW (X) pontrahúzható komplexus (2.17. Következmény).
Ötlet: A 14.10. Feladat miatt létezik egy CW-homotópia f és g között,
Whitehead tétele (14.13. Tétel) miatt h egy homotóp ekvivalencia.
Ezért a lemma következik a 15.9. Tételből és a 15.10. Feladatból. □
15.12. Megjegyzés. Legyenek X, Y CW-komplexusok, f : X → Y
tetszőleges folytonos függvény! A 14.7. Tétel miatt f homotóp egy
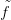 : X → Y CW-függvényhez. A Δ⋅CW (
: X → Y CW-függvényhez. A Δ⋅CW (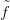 ) lánc-leképezés függ a
) lánc-leképezés függ a 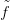 választásától, de a 14.10. Feladat miatt bármely két választás lánc-homotóp
leképezéseket ad. Jelöljük f∗-gal a Δ⋅CW (
választásától, de a 14.10. Feladat miatt bármely két választás lánc-homotóp
leképezéseket ad. Jelöljük f∗-gal a Δ⋅CW (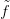 ) homotópia osztályát! A
14.7. Tételből és a 14.10. Feladatból következik, hogy
) homotópia osztályát! A
14.7. Tételből és a 14.10. Feladatból következik, hogy
-
(a)
- f∗ csak az [f] homotópia-osztálytól függ,
-
(b)
- ha g : Y → Z egy másik folytonos függvény, akkor (g∘f)∗ = g∗∘f∗,
-
(c)
- ha f homotóp ekvivalencia, akkor f∗ is homotóp ekvivalencia,
-
(d)
- ha X pontrahúzható, akkor Δ⋅CW (X) is pontrahúzható.
15.13. Megjegyzés. Az előző megjegyzés tovább pontosítható: Δ⋅CW
kiterjeszthető Top CW -ből az Abel csoportok derivált kategóriájába menő
funktorrá. Ez a funktor homotópia-invariáns, tehát indukál egy funktort
a homotópia kategóriából az Abel csoportok derivált kategóriájába.
15.14. Definíció. Legyen G egy Abel csoport. Definiáljuk a G-együtthatós
CW-homológia és a CW-kohomológia funktorokat:
Mindent általánosíthatunk CW-párokra is:
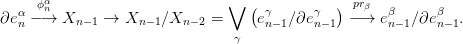
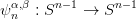
![∂ ( ) ∑
ΔCWn (X )− → ΔCWn− 1(X ) , ∂ [eαn] = deg(ψnα,β) ⋅ [eβn− 1].
β](algebrai-topologia271x.png)
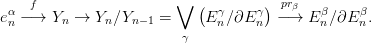
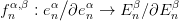
![f∗ ∑
ΔCWn (X ) −→ ΔCWn (Y ) , f∗[eαn] = deg(fαn,β) ⋅ [E βn].
β](algebrai-topologia274x.png)
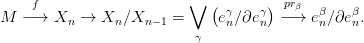
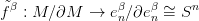
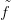

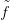
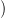
![∑
f [M ] = deg(f˜β) ⋅ [eβ].
∗ n
β](algebrai-topologia281x.png)
![( )
∂ f [M ] = f [∂M ],
∗ ∗](algebrai-topologia282x.png)
![( )
ha M zárt, akkor ∂ f∗[M ] = 0.](algebrai-topologia283x.png)
![( )
f∗[B ] = f∗[M ] és f∗[∂B ] = ∂ f ∗[M ] .](algebrai-topologia284x.png)
![f ∗[∂N ] = 0.](algebrai-topologia285x.png)
![f∗[∂M ] − f∗[∂B ] = f∗[∂N ] = 0.](algebrai-topologia286x.png)

![]](algebrai-topologia288x.png)

![]](algebrai-topologia290x.png)

![]](algebrai-topologia292x.png)

![]](algebrai-topologia294x.png)

![]](algebrai-topologia296x.png)


![(
Ln [eαn]) = h∗[eαn × [0,1 ]].](algebrai-topologia301x.png)
![( )
∂ eαn × [0,1] = ∂eαn × [0,1] ∪ en α × {0} ∪ enα × {1}.](algebrai-topologia302x.png)
![( α [ α ]
∂Ln [en]) = ∂h∗ en × [0,1] = h∗[∂B ] =](algebrai-topologia303x.png)
![[ α ] [ ] [ ] ( )
= h ∗∂e n× [0,1 ]+h ∗ enα ×{0 } +h ∗ enα× {1} = Ln −1 ∂[en] +f ∗[en]− g∗[en]](algebrai-topologia304x.png)