18.1. Definíció. Legyen X egy szimplíciális komplexus, vagy még általánosabban, egy delta-komplexus. Mivel a szimplexek egyben cellák is, X tekinthető CW-komplexusnak is. Az X szimplíciális lánc-komplexusa:
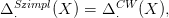
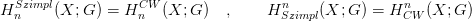
18.1. Definíció. Legyen X egy szimplíciális komplexus, vagy még általánosabban, egy delta-komplexus. Mivel a szimplexek egyben cellák is, X tekinthető CW-komplexusnak is. Az X szimplíciális lánc-komplexusa:
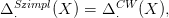
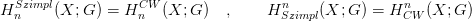
18.2. Megjegyzés. Még általánosabb fogalom: a szimplíciális halmazok. Íme, egy másik bevezető.
18.3. Megjegyzés. A 16.4. Megjegyzés alapján könnyen látható, hogy Δ⋅simpl tisztán kombinatórikai objektum, míg Δ ⋅ és Δ⋅CW a topológiában élnek.
18.4. Megjegyzés. Ebben a jegyzetben nem foglalkozunk szimplíciális homológiával, de érdemes megjegyezni, hogy a 17.6. Feladat állítása átfogalmazható: az X szimplíciális lánc-komplexusa, Δ⋅simpl(X), lánc-homotóp az X szinguláris lánc-komplexusával, tehát a megfeleő homológia- és kohomológia-csoportok izomorfak.