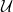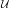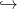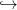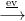16. Szinguláris szimplexek
16.1. Definíció. Tekintsük az ℝn+1 térben az e
i bázis-vektorok által
kifeszített n-dimenziós szimplexet — a csúcsokat az ei-kkel azonos
sorrendben írjuk, ez adja az irányítást. Ezt a szimplexet Δn-nel jelöljük,
és standard n-szimplexnek hívjuk.
16.2. Definíció. Legyen X egy topológikus tér. Egy n-dimenziós
n-dimenziós szinguláris szimplex X-ben nem más, mint egy folytonos
függvény ϕ : Δn → X. A ϕ-nek n + 1 oldala van, ezek a következő
(n − 1)-dimenziós szimplexek. Minden 0 ≤ i ≤ n értékre tekintjük
azt a Δn−1 → Δn lineáris leképezést, amelyik az e
0,e1,…ei−1 ∈ Δn−1
csúcsokat Δn ugyanilyen nevű csúcsaiba képezi, az e
i,ei+1,…en−1 ∈Δn−1
csúcsokat pedig rendre az ei+1,ei+2,…en ∈ Δn csúcsokba viszi. Ezt a
lineáris leképezést ϕ-vel komponálva megkapjuk ϕ i-edik oldalát, ∂iϕ-t.
16.3. Definíció. Definiáljuk az S funktort, ami topológikus terekhez
CW-komplexusokat rendel. Legyen X egy topológikus tér. S(X)
n-szimplexei éppen az X-beli n-dimenziós szinguláris szimplexek
lesznek, a ragasztást pedig dimenzió szerinti indukcióval definiáljuk.
Legyen ϕ egy szinguláris n-szimplex, és tegyük fel, hogy az S(X)
komplexus (n − 1)-vázát már elkészítettük. Minden 0 ≤ i ≤ n értékre
a ∂iϕ oldal egy (n − 1)-dimenziós szimplex, tehát benne van az (n −
1)-vázban. Ragasszuk hát ϕ i-edik oldalát ehhez az (n − 1)-szimplexhez!
Az S(X) komplexus szimplexei folytonos függvények X-be. Ezek
a függvények a ragasztások mentén jól illeszkednek egymáshoz, tehát
összeállnak egy ev : S(X) → X folytonos függvénnyé, amit
kiértékelésnek hívunk.
16.4. Megjegyzés. A 16.3. Definícióban többet is kapunk: egy
delta-komplexust építünk fel. A CW-komplexusban megengedünk
tetszőleges folytonos ragasztásokat, tehát ezek topológiai objektumok.
Ezzel szemben delta-komplexusban viszont élet élhez, háromszöget
háromszöghöz, n-szimplexet n-szimplexhez illesztünk, lineáris
ragasztó leképezéssel, ezért a delta-komplexusok tisztán kombinatórikai
objektumok, amelyeknek van topológiai realizációja. Ebben a jegyzetben
elegendő a CW struktúrát ismerni.
16.5. Tétel. Legyen X egy topológikus tér. Az ev : S(X) → X
kiértékelés egy gyenge homotóp ekvivalencia.
Bizonyítás. Be kell látni, hogy ev ∗ : πn S(X)
S(X)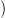 → πn(X) izomorfizmus
minden n-re. Választunk Sn-en egy szimplex-felbontást. Ennek
segítségével minden f : Sn → X folytonos leképezés felemelhető egy
→ πn(X) izomorfizmus
minden n-re. Választunk Sn-en egy szimplex-felbontást. Ennek
segítségével minden f : Sn → X folytonos leképezés felemelhető egy
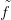 : Sn → S(X) folytonos függvénnyé, amelyre ev ∘
: Sn → S(X) folytonos függvénnyé, amelyre ev ∘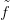 = f, tehát ev
∗
szürjektív.
= f, tehát ev
∗
szürjektív.
Legyenek most 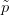 ,
,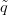 : Sn → S(X) folytonos függvények, és h :
S × [0, 1] → X egy homotópia ev ∘
: Sn → S(X) folytonos függvények, és h :
S × [0, 1] → X egy homotópia ev ∘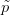 és ev ∘
és ev ∘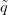 között. Először
lecseréljük
között. Először
lecseréljük 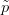 -t és
-t és 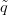 -t egy-egy szimplíciális approximációra. Ez ad Sn×
{0}-án és Sn ×{1}-en egy-egy szimplex-felbontást, amit kiterjesztünk
Sn × [0, 1] szimplex-felbontásává. Ennek segítségével gyártunk olyan
-t egy-egy szimplíciális approximációra. Ez ad Sn×
{0}-án és Sn ×{1}-en egy-egy szimplex-felbontást, amit kiterjesztünk
Sn × [0, 1] szimplex-felbontásává. Ennek segítségével gyártunk olyan
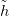 : Sn × [0, 1] → S(X) függvényt, amelyre ev ∘
: Sn × [0, 1] → S(X) függvényt, amelyre ev ∘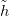 = h. Tehát ev
∗
injektív. □
= h. Tehát ev
∗
injektív. □
16.6. Tétel.
-
(a)
- S : Top → Top CW egy kovariáns funktor. (11.2. Definíció,
14.3. Definíció).
-
(b)
- Ha f és g homotóp folytonos függvények, akkor S(f) és S(g)
között van egy CW-homotópia.
-
(c)
- Ha f gyenge homotóp ekvivalencia, akkor S(f) egy CW-függvény,
amelyik homotóp ekvivalencia.
-
(d)
- Ha az X tér olyan, hogy πn(X) = {1} minden n-re, akkor S(X)
pontrahúzható (topológikus térként).
Bizonyítás. Ha σ egy szinguláris szimplex X-ben, és komponáljuk
őt egy f és g közötti homotópiával, akkor az f(σ) és g(σ)
szinguláris szimplexek közti homotópiát kapunk. Ezek a homotópiák
összeragadnak egy S(f) és S(g) közötti CW-homotópiává. A többi
állítás azonnal következik Whitehead tételéből (14.13. Tétel) és a
16.5. Tételből. □
16.8. Megjegyzés. A 16.7. Lemmának számtalan,
ugyanezzel a technikával bizonyítható változata van. Például, ha X egy
differenciálható sokaság, akkor tekinthetjük a differenciálható szimplek
részkomplexusát, ha pedig X egy metrikus tér, akkor tekinthetjük az
ε-nál kisebb átmérőjű szimplexek részkomplexusát — ezek is homotóp
ekvivalensek X-szel és S(X)-szel.
 S(X)
S(X)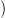 → πn(X) izomorfizmus
minden n-re. Választunk Sn-en egy szimplex-felbontást. Ennek
segítségével minden f : Sn → X folytonos leképezés felemelhető egy
→ πn(X) izomorfizmus
minden n-re. Választunk Sn-en egy szimplex-felbontást. Ennek
segítségével minden f : Sn → X folytonos leképezés felemelhető egy
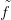 : Sn → S(X) folytonos függvénnyé, amelyre ev ∘
: Sn → S(X) folytonos függvénnyé, amelyre ev ∘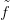 = f, tehát ev
∗
szürjektív.
= f, tehát ev
∗
szürjektív.
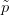 ,
,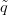 : Sn → S(X) folytonos függvények, és h :
S × [0, 1] → X egy homotópia ev ∘
: Sn → S(X) folytonos függvények, és h :
S × [0, 1] → X egy homotópia ev ∘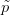 és ev ∘
és ev ∘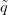 között. Először
lecseréljük
között. Először
lecseréljük 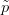 -t és
-t és 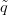 -t egy-egy szimplíciális approximációra. Ez ad Sn×
{0}-án és Sn ×{1}-en egy-egy szimplex-felbontást, amit kiterjesztünk
Sn × [0, 1] szimplex-felbontásává. Ennek segítségével gyártunk olyan
-t egy-egy szimplíciális approximációra. Ez ad Sn×
{0}-án és Sn ×{1}-en egy-egy szimplex-felbontást, amit kiterjesztünk
Sn × [0, 1] szimplex-felbontásává. Ennek segítségével gyártunk olyan
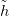 : Sn × [0, 1] → S(X) függvényt, amelyre ev ∘
: Sn × [0, 1] → S(X) függvényt, amelyre ev ∘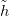 = h. Tehát ev
∗
injektív. □
= h. Tehát ev
∗
injektív. □