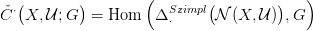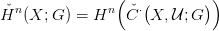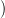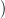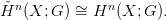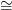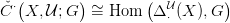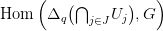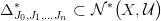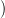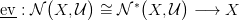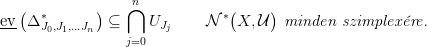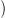19. Čech kohomológia
19.1. Definíció. Egy X topológikus tér {Ui}i∈I nyílt fedését jó
fedésnek mondjuk, ha minden J ⊆ I véges részhalmazra a {Ui}i∈I
metszet vagy üres, vagy pontrahúzható.
19.4. Megjegyzés. A 19.3. Definíció csak akkor használható, ha az
X térnek létezik jó fedése. Természetesen létezik ennél általánosabb
definíció is, de nekünk most elég ez a speciális eset.
Először adunk egy algebrai bizonyítást, utána egy geometriait. A
geometriai bizonyítás hosszabb, de elemibb.
Algebrai bizonyítás. Elég az izomorfizmust belátni, abból már
következik a függetlenség is. Idézzük fel a 16.7. Lemmában szereplő
S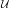 (X) ⊆ S(X) rész-komplexust! Ehhez tartozik egy Δ
⋅
(X) ⊆ S(X) rész-komplexust! Ehhez tartozik egy Δ
⋅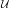 (X) ≤
Δ⋅(X) részkomplexust, melyet a S
(X) ≤
Δ⋅(X) részkomplexust, melyet a S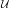 (X)-beli szimplexek generálnak. A
16.7. Lemma miatt Δ⋅
(X)-beli szimplexek generálnak. A
16.7. Lemma miatt Δ⋅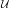 (X)
(X)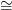 Δ
⋅(X) lánc-ekvivalensek. A 19.5. Tétel
tehát azonnal következik az alábbi lánc-ekvivalenciából:
Δ
⋅(X) lánc-ekvivalensek. A 19.5. Tétel
tehát azonnal következik az alábbi lánc-ekvivalenciából:
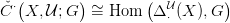
Abban az esetben, ha
egyetlen nyílt halmazból áll, ez következik a
17.3. Tétel (
d) pontjából. Az általános eset pedig azonnal következik a
3.24. Következményből, csak a megfelelő kettős komplexust kell kitölteni
— amit az olvasóra bízunk!
□
19.6. Feladat. Töltsd ki az előző bizonyítás végén felbukkanó kettős
komplexust! Lásd be, hogy a sorok és az oszlopok valóban egzaktak!
Ötlet: Minden (p + 1)-elemű J ⊆ I részhalmazhoz készítsd el a
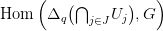
csoportot. Ezek direkt szorzata (rögzített
p,q értékre) legyen a
3.24. Következményben
keresett
Mp,q csoport! Lásd be a sorok és az oszlopok egzaktságát! Az
egzaktság bizonyításában felhasználhatod, hogy a tétel igaz abban az
esetben, amikor
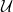
egyelemű.
□
19.7. Konstrukció. Legyen X egy topológikus tér, és 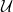 = {Ui}i∈I
egy jó fedése. Jelölje
= {Ui}i∈I
egy jó fedése. Jelölje 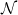 ∗
∗ X,
X,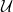
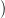 az
az 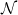
 X,
X,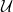
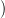 komplexus súlyponti
felosztását. Tetszőleges J0 ⊂ J1 ⊂
komplexus súlyponti
felosztását. Tetszőleges J0 ⊂ J1 ⊂  ⊂ Jn ⊆ I véges
részhalmaz-sorozatra jelölje
⊂ Jn ⊆ I véges
részhalmaz-sorozatra jelölje
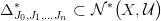 azt a szimplexet, amit az
azt a szimplexet, amit az 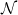
 X,
X,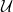
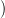 -beli ΔJ0 ⊂ ΔJ1 ⊂ ΔJ2
-beli ΔJ0 ⊂ ΔJ1 ⊂ ΔJ2 ⊂
ΔJn egymásba ágyazott szimplexek súlypontjai feszítenek ki. Dimenzió
szerinti indukcióval építünk egy
⊂
ΔJn egymásba ágyazott szimplexek súlypontjai feszítenek ki. Dimenzió
szerinti indukcióval építünk egy
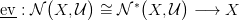 folyonos leképezést az alábbi tulajdonsággal:
folyonos leképezést az alábbi tulajdonsággal:
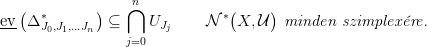 | (4) |
Tegyük fel, hogy a ΔJ0,J1,…Jn∗ szimplex peremén már elkészült az ev
függvény, és ott teljesíti a (4) követelményt. Mivel a ⋂
j=0nU
Jj nyílt halmaz
pontrahúzható, a függvénytkönnyű beterjeszteni a szimplex belsejébe
is.
Bizonyítás. Elég a (b) állítást bizonyítani, az (a) ennek speciális
esete (üres A-val). A feltétel miatt f az A minden szimplexét
beleképezi valamelyik 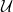 -beli nyílt halmazba. A Lebesgue Lemma
segítségével az A komplementerében lévő szimplexeket is felbontjuk
kisebb szimplexekre úgy, hogy f az új szimplexek mindegyikét
beleképezze valamelyik
-beli nyílt halmazba. A Lebesgue Lemma
segítségével az A komplementerében lévő szimplexeket is felbontjuk
kisebb szimplexekre úgy, hogy f az új szimplexek mindegyikét
beleképezze valamelyik 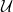 -beli nyílt halmazba. Jelölje Ỹ az Y teret ezzel
az új szimplex felbontással, Ỹ∗ pedig az Ỹ súlyponti felosztását. Mivel
f(Ỹ∗) kompakt, van olyan Ĩ ⊂ I véges részhalmaz, melyre {U
i}i∈Ĩ
lefedi f(Ỹ∗)-ot. Először definiáljuk a ϕ függvényt az Ỹ∗ csúcsain.
-beli nyílt halmazba. Jelölje Ỹ az Y teret ezzel
az új szimplex felbontással, Ỹ∗ pedig az Ỹ súlyponti felosztását. Mivel
f(Ỹ∗) kompakt, van olyan Ĩ ⊂ I véges részhalmaz, melyre {U
i}i∈Ĩ
lefedi f(Ỹ∗)-ot. Először definiáljuk a ϕ függvényt az Ỹ∗ csúcsain.
Legyen P az Ỹ∗ tetszőleges csúcsa, tehát egy σ ⊆ Y szimplex
súlypontja. Jelölje Jσ ⊆ Ĩ azon j ∈ Ĩ indexek halmazát, melyekre
f(σσ) ⊆ Uj. Legyen ϕ(P) a ΔJσ ⊆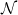 (X,
(X,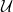 ) szimplex súlypontja, ami
az
) szimplex súlypontja, ami
az 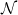 ∗(X,
∗(X,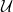 ) komplexus egyik csúcsa.
) komplexus egyik csúcsa.
Legyen most δ az Ỹ∗ tetszőleges n-szimplexe. Enne csúcsai bizonyos
σ0 ⊂ σ1 ⊂ ⊂ σn Ỹ-beli szimplexek súlypontjai. A ϕ függvény a δ
csúcsait éppen a ΔJσ
0,Jσ1,…Jσn
⊂ σn Ỹ-beli szimplexek súlypontjai. A ϕ függvény a δ
csúcsait éppen a ΔJσ
0,Jσ1,…Jσn 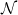 ∗(X,
∗(X,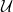 )-beli szimplex csúcsaiba viszi,
kiterjesztjük lineárisan az egész δ szimplexre. Ezt minden szimplexre
elvégezve megkapjuk a keresett ϕ függvényt. □
)-beli szimplex csúcsaiba viszi,
kiterjesztjük lineárisan az egész δ szimplexre. Ezt minden szimplexre
elvégezve megkapjuk a keresett ϕ függvényt. □
19.10. Feladat. Lásd be, hogy a 19.9. Lemma bizonyításában a ϕ
függvény jól definiált! ha δ1,δ2 két szimplex Ỹ-ban, akkor a δ1-re való
kiterjesztés a δ1 ∩δ2 szimplexen megegyezik a δ2-re való kiterjesztéssel.
Ötlet: Ha δ1 a δ szimplex egyik oldala, akkor ϕ-t a δ1 szimplexen
kétféleképpen is definiáltuk: δ-ra, illetve δ1-ra való kiterjesztéssel.
Miért ugyanaz a két kiterjesztés? □
19.11. Feladat. Lásd be, hogy a 19.9. Lemma bizonyításában a ϕ
függvény az A halmazon megegyezik ϕA-val!
A 19.5. Tétel geometriai bizonyítása. Azonnal következik a
definícióból és a 19.12. Következményből. □
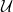 = {Ui}i∈I
nyílt halmazok egy rendszere. Az
= {Ui}i∈I
nyílt halmazok egy rendszere. Az 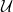 idege a következő,
idege a következő, 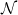
 X,
X,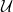
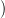 -vel
jelölt szimplíciális komplexus: Minden (n + 1)-elemű J ⊆ I
részhalmazhoz, amelyre ⋂
i∈JUi≠∅ tartozik egy ΔJ-vel jelölt n-szimplex,
melynek csúcsait megcímkézzük J elemeivel. Ezért n ≥ 1 esetén a ΔJ
minden oldalán egy n-elemű J′ ⊂ J részhalmazt olvashatunk: ezt az
oldalt a ΔJ′ szimplexhez ragasztjuk, mégpedig úgy, hogy az azonosan
címkézett csúcsok illeszkedjenek egymáshoz.
-vel
jelölt szimplíciális komplexus: Minden (n + 1)-elemű J ⊆ I
részhalmazhoz, amelyre ⋂
i∈JUi≠∅ tartozik egy ΔJ-vel jelölt n-szimplex,
melynek csúcsait megcímkézzük J elemeivel. Ezért n ≥ 1 esetén a ΔJ
minden oldalán egy n-elemű J′ ⊂ J részhalmazt olvashatunk: ezt az
oldalt a ΔJ′ szimplexhez ragasztjuk, mégpedig úgy, hogy az azonosan
címkézett csúcsok illeszkedjenek egymáshoz.