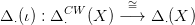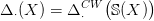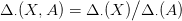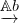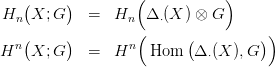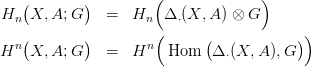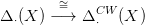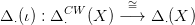Szingularis lanc-komplexus, homologia es kohomologia

17.1. Definíció. A szinguláris lánc-komplexus funktor az S funktor és a CW-lánc-komplexus funktor kompozíciója. Tehát a topológikus terek kategóriájából (11.2. Definíció) képez az Abel csoport kompexusok kategóriájába, egy X topológikus térhez az alábbi komplexust rendeli:

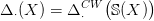CW ( ) Δ⋅(X ) = Δ ⋅ S(X )

Általánosabban, egy (X,A) tér-pár szinguláris lánc-komplexusa:

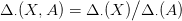
∕ Δ ⋅(X, A ) = Δ ⋅(X ) Δ ⋅(A )

17.2. Megjegyzés. Sok-sok egymással (többé-kevésbé) lánc-homotóp funktort használunk, a jelölésük is nagyon hasonló: Δ⋅, Δ⋅^CW, Δ ⋅^Szimpl, stb. Ebben a jegyzetben a szinguláris láncokkal tudunk legkényelmesebben dolgozni, azért azt jelöljük Δ⋅-val, megkülönböztető kitevő nélkül.

17.3. Tétel.

(a): Δ⋅ : Top → 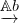egy kovariáns funktor. (11.2. Definíció, 2.2. Definíció).
(b): Ha f,g homotóp függvények, akkor Δ⋅(f) és Δ⋅(g) lánc-homotópok.
(c): Ha egy h függvény gyenge homotóp ekvivalencia, akkor Δ⋅(h) egy lánc-ekvivalencia.
(d): Ha az X tér olyan, hogy π_n(X) = {1} minden n-re, akkor Δ⋅(X) pontrahúzható komplexus (2.17. Következmény).

17.4. Definíció. Legyen G egy Abel csoport. Definiáljuk a G-együtthatós szinguláris homológia és a szinguláris kohomológia funktorokat.

( ) ( ) Hn X; G = Hn Δ ⋅(X ) ⊗ G ( ) ( ( )) Hn X; G = Hn Hom Δ ⋅(X ),G

Mindent általánosíthatunk tér-párokra is:

( ) Hn (X, A;G ) = Hn Δ ⋅(X, A ) ⊗ G ( ) n( ) n ( ) H X, A;G = H Hom Δ ⋅(X, A ),G

Tekintsük azt a ko-láncot, amelyik minden 0-dimenziós szimplexhez ugyanazt a g ∈ G elemet rendeli — ezt is g-vel fogjuk jelölni (mint a konstans függvényeket). Ez egy ko-ciklus, tehát megad egy konstans kohomológia-osztályt, amit szintén g-vel jelölünk:

g ∈ H0 (X, A; G ) minden g ∈ G -re.

Ebben a jegyzetben, ha mindenféle jelző nélkül homológiát illetve kohomológiát írunk, akkor az mindig a szinguláris homológiát illetve a szinguláris kohomológiát jelenti.

17.5. Tétel. Legyen X egy CW-komplexus. Létezik egy

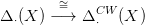∼ Δ (X )−=→ ΔCW (X ) ⋅ ⋅

természetes lánc-ekvivalencia.

Bizonyítás. A 16.5. Tétel szerint ev : S(X) → X egy gyenge homotóp ekvivalencia. Erre alkalmazzuk a Δ⋅^CW funktort, a 15.11. Tétel miatt lánc-ekvivalenciát kapunk. □

17.6. Feladat. Legyen X egy szimplíciális komplexus, vagy még általánosabban, egy delta-komplexus. A szimplex felbontás ad egy természetes ι : X → S(X) beágyazást. Mutasd meg, hogy ι és ev (16.3. Definíció) egymás homotópia inverzei!

Tekintsük X szimplex-felbontását egy CW-felbontásnak. Az ι segítségével a 17.5. Tételbeli lánc-ekvivalencia inverze sokkal könnyebben számolható:

CW ∼= Δ ⋅(ι) : Δ ⋅ (X )−→ Δ ⋅(X )

17. Szinguláris lánc-komplexus, homológia és kohomológia