25.1. Tétel (Künneth formula kohomológiára — I). Legyenek X és Y topológikus terek, F egy test. Ekkor a külső szorzat (lásd a 24.1. Konstrukciót) izomorfizmust indukál:
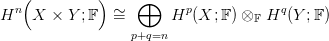
Künneth formulái segítségével topológikus terek direkt szorzatának a homológia- illetve kohomológia-csoportjait számíthatjuk ki. Ebben a fejezetben csak kohomológia-csoportokkal foglalkozunk. Természetesen léteznek ezekkel analóg, homológia-csoportokra vonatkozó formulák is, amelyek ugyanilyen módon bizonyíthatók.
25.1. Tétel (Künneth formula kohomológiára — I). Legyenek X és Y topológikus terek, F egy test. Ekkor a külső szorzat (lásd a 24.1. Konstrukciót) izomorfizmust indukál:
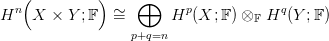
Bizonyítás. Következik a 9.2. Feladat állításából. □
25.2. Tétel (Künneth formula kohomológiára — II). Legyenek X és Y topológikus terek, M és N modulusok az R gyűrű felett. Tegyük fel, hogy Hq(Y ; R) szabad R-modulus minden q-ra. Ekkor a külső szorzat (lásd a 24.1. Konstrukciót) izomorfizmust indukál:

Bizonyítás. Következik a 9.7. Tételből. □