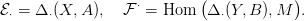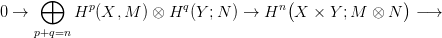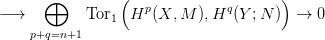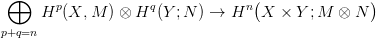26. Általános Künneth tételek — topológia
Ötlet: Alkalmazzuk a 10.4. Tételt az következő szereposztásban:
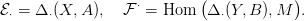 □
□
26.2. Feladat. Fogalmazd meg, és bizonyítsd be a 26.1. Tétel
tér-párokra vonatkozó általánosítását!
26.3. Tétel (Künneth egzakt sorozat kohomológiára). Legyenek X, Y
topológikus terek, R nullosztómentes főideálgyűrű, M, N R-modulusok.
Tegyük fel, hogy az alábbi végességi feltételek közül legalább az egyik
teljesül:
-
—
- Hn(X; ℤ) és Hn(Y ; ℤ) végesen generált minden n-re,
-
—
- Hn(X; ℤ) végesen generált, minden n-re, és N is végesen generált.
Ekkor létezik az alábbi funktoriális rövid egzakt sorozat:
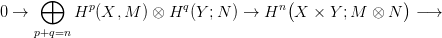
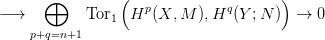 Ez
a sorozat (nem kanonikusan) felhasad.
Ez
a sorozat (nem kanonikusan) felhasad.
Ötlet: Használd Eilenberg-Zilber tételt (22.1. Tétel), a 4.9. Lemmát, a
23.3. Tétel bizonyításában szereplő (7) azonosságot, és a 10.2. Tételt.
□
26.4. Feladat. Fogalmazd meg, és bizonyítsd be a 26.3. Tétel
tér-párokra vonatkozó általánosítását!
26.5. Feladat. Lásd be, hogy a 26.3. Tételben szereplő
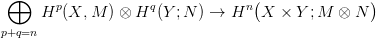 homomorfizmus nem más, mint a külső szorzás (24.1. Konstrukció).
homomorfizmus nem más, mint a külső szorzás (24.1. Konstrukció).
26.6. Feladat. Ha R test, akkor a 26.3. Tétel ad egy
 izomorfizmust (feltéve, hogy a végességi feltétel teljesül). Lásd be, hogy
ez ugyanaz az izomorfizmus, mint amit a 26.1. Tétel ígér. (Sőt, a
26.5. Feladat alapján ez megegyezik a külső szorzással is.)
izomorfizmust (feltéve, hogy a végességi feltétel teljesül). Lásd be, hogy
ez ugyanaz az izomorfizmus, mint amit a 26.1. Tétel ígér. (Sőt, a
26.5. Feladat alapján ez megegyezik a külső szorzással is.)
26.7. Feladat. Fogalmazd meg, és bizonyítsd be a Künneth formulák
(26.1 és 26.3) homológia-csoportokra vonatkozó variánsát. (Használd a
10.2. Tételt!)

 X; Hq
X; Hq Y ; M
Y ; M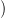

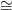 Hp(X; R) ⊗ Hq(X; M), és a
fenti izomorfizmus inverze éppen a külső szorzat (24.1. Konstrukció,
összegezve p + q = n-re).
Hp(X; R) ⊗ Hq(X; M), és a
fenti izomorfizmus inverze éppen a külső szorzat (24.1. Konstrukció,
összegezve p + q = n-re).