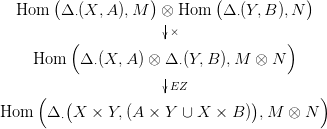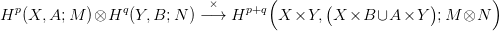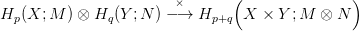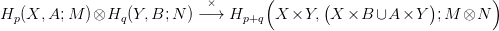Kulső szorzas — topologia

24.1. Konstrukció (Külső szorzat — kohomológia). Tetszőleges X és Y topológikus térekhez, M és N modulusokhoz, p,q egészekhez hozzárendelünk egy

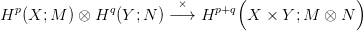
( ) Hp (X; M ) ⊗ Hq (Y ;N )− ×→ Hp+q X × Y ;M ⊗ N

külső szorzás homomorfizmust (angolul:cross product), ami minden változójában természetes transzformáció. A hozzárendelés az alábbi, tér-párokra vonatkozó konstrukció speciális esete, A = B = ∅ választással.

Legyenek (X,A) és (Y,B) olyan tér-párok (11.1. Definíció), melyekre {X × B,A × Y } jól vág (21.2. Definíció), és legyenek M, N modulusok. Tekintsük az alábbi diagramot, ahol az első lánc-homomorfizmus a 8.4. Feladatbeli külső szorzás, a másodikat pedig az Eilenberg-Zilber tételből (22.2. Következmény) kapjuk:

Hom (Δ (X, A ),M ) ⊗ Hom (Δ (Y, B ),N ) ⋅ | ⋅ ( × ) Hom Δ ⋅(X, A ) ⊗ Δ ⋅(Y, B ),M ⊗ N | ( EZ ) ( ) Hom Δ ⋅ X × Y, (A × Y ∪ X × B ) ,M ⊗ N

Ha a kompozícióra alkalmazzuk a homológia funktort, és használjuk a 8.1. Tétel, akkor a külső szorzás (angolul:cross product) homomorfizmushoz jutunk:

( ) Hp (X, A;M )⊗Hq (Y, B; N )−×→ Hp+q X ×Y, (X ×B ∪A ×Y );M ⊗N

Ez minden változójában természetes transzformáció.

24.2. Feladat (Külső szorzat — homológia). A 24.1. Konstrukció mintájára konstruáld meg az alábbi külső szorzás homomorfizmusokat:

( ) × Hp(X; M ) ⊗ Hq (Y ;N )− → Hp+q X × Y;M ⊗ N

× ( ( ) ) Hp (X,A; M )⊗Hq (Y, B;N ) −→ Hp+q X ×Y, X ×B ∪A ×Y ;M ⊗N

24. Külső szorzás — topológia