Kunneth Formulak

9.2. Feladat. Adott egy F test, legyenek ^⋅ és ^⋅ vektortér-komplexusok az F felett. Lásd be, hogy a külső szorzás (8.1. Tétel) ebben az esetben izomorfizmust indukál:

(---------⋅) ⊕ Hn K ⋅ ⊗ F L ⋅ = Hp (K ⋅) ⊗F Hq (L⋅) p+q=n

Az előző két feladatot szeretnénk gyűrűkre általánosítani: a külső szorzás segítségével megpróbáljuk kiszámolni a direkt szorzat komplexus homológiáit. Mi most az egész számok gyűrűjére szorítkozunk, abel csoport együtthatókat használunk. (Az általános esethez nézd meg a Künneth spektrális sorozatot.)

9.3. Lemma. Adott egy R főideálgyűrű. Legyen ^⋅ egy szabad R-modulusokból épült komplexus, tegyük fel, hogy Hⁿ(^⋅) is szabad minden n-re. Legyen 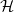^⋅ az a komplexus, melyben 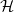ⁿ = Hⁿ(^⋅), és a differenciálja nulla. Ekkor létezik egy 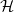^⋅ = ^⋅⊕^⋅ felbontás, amelyben a ^⋅ részkomplexus pontrahúzható (2.17. Következmény). Megjegyezzük, hogy ez a felbontás egyáltalán nem kanonikus!

Bizonyítás. Jelölje d a ^⋅ komplexus differenciálját. A 2.1. Definíció miatt Im(d)^⋅ ≤ Ker(d)^⋅ ≤^⋅ rész-komplexusok. Tekintsük a következő rövid egzakt sorozatokat:

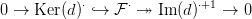
⋅ ⋅ ⋅+1 0 → Ker(d) `→ F ↠ Im (d) → 0

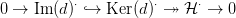
0 → Im (d)⋅ `→ Ker(d)⋅ ↠ H ⋅ → 0

Világos, hogy a

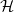^⋅ hányados komplexus differenciálja nulla, és a 2.3. Definíció miatt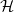

ⁿ = Hⁿ(

), ami egy szabad R-modulud. A 4.4. Tények (h) pontja miatt Ker(d)^⋅és Im(d)^⋅ is szabad R-modulusokból állnak. Egyszerű diagram vadászat mutatja, hogy mindkét egzakt sorozat felhasad (nem kanonikusan). Ezért

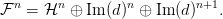
n n n n+1 F = H ⊕ Im (d) ⊕ Im (d) .

Könnyen látható, hogy az Im(d)ⁿ⊕Im(d)ⁿ⁺¹ összeadandók egy részkomplexust alkotnak, ami izomorf az Im(d)^⋅ id
−→

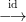Im(d)^⋅ izomorfizmus leképezés-kúpjával. A 3.15. Lemma bizonyításában láttuk, hogy egy ilyen leképezés-kúp pontrahúzható. □

9.5. Tétel. Legyenek R egy főideálgyűrű, 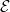_⋅ és _⋅ R-modulus komplexusok. (Alsó indexeket használunk, lásd az 1.2. Konvenciót.) Tegyük fel, hogy _n és H_n(_⋅) szabad R-modulusok minden n-re. Ekkor a külső szorzás (8.1. Tétel) egy izomorfizmust ad:

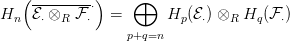
( --------⋅) ⊕ Hn E⋅ ⊗R F ⋅ = Hp (E⋅) ⊗R Hq (F ⋅) p+q=n

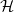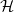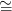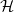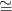
Bizonyítás. A 9.3. Lemma ad egy _⋅ = _⋅ ⊕_⋅ felbontást, ahol a _⋅ részkomplexus differenciálja nulla, ^⋅ pedig pontrahúzható (lásd a 2.17. Következményt). Látható, hogy H_n(_⋅)H_n(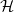_⋅)_n. Másrészt pedig

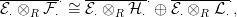
--------⋅ ∼ --------⋅ --------⋅ E⋅ ⊗R F⋅ = E⋅ ⊗R H ⋅ ⊕ E⋅ ⊗R L ⋅,

és az

_⋅⊗_R

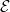_⋅^⋅ tag pontrahúzható (lásd alább a 9.6. Feladatot). A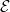

_⋅⊗ _R

_⋅ kettős komplexusban a vízszintes differenciál (a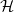

_⋅-ből származó, lásd a 3. ábrán) nulla, ebből következik az alábbi direkt összeg felbontás:

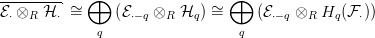
⊕ ⊕ E--⊗--H--⋅ ∼= (E ⊗ H ) ∼= (E ⊗ H (F )) ⋅ R ⋅ ⋅−q R q ⋅−q R q ⋅ q q

ahol a ⋅− q index azt jelenti, hogy az eredeti komplexusban minden komponens fokszámát q-val csökkentjük. Használva, hogy H_q(

_⋅) szabad R-modulus, az alábbi könnyű számolás mutatja a tétel igaz voltát:

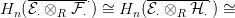
--------⋅ --------⋅ Hn (E⋅ ⊗R F⋅) ∼= Hn (E⋅ ⊗R H ⋅) ∼=

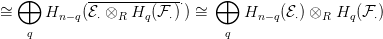
⊕ ⊕ ∼= H (E-⊗---H--(F--)⋅) ∼= H (E ) ⊗ H (F ) n−q ⋅ R q ⋅ n−q ⋅ R q ⋅ q q

□

9.6. Feladat. Lásd be, hogy ha 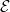_⋅, _⋅ R-modulus komplexusok, és _⋅ pontrahúzható, akkor 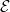_⋅⊗_⋅^⋅ is pontrahúzható! (Ezt használtuk a 9.5. Tétel bizonyításában.)

9.7. Tétel. Legyenek R egy főideálgyűrű, 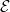_⋅ és ^⋅ R-modulus komplexusok. (Alsó és felső indexeket is használunk, lásd az 1.2. Konvenciót.) Legyen továbbá M egy R-modulus. Tegyük fel, hogy ⁿ és Hⁿ(^⋅) szabad R-modulusok minden n-re. Ekkor a külső szorzás (8.5. Feladat) egy izomorfizmust ad:

(-------------------⋅) ⊕ ( ) Hn HomR (E⋅,F ⋅ ⊗R M ∼= HomR Hp (HomR (E⋅,M )),Hq (F ⋅) p+q=n

9. Künneth Formulák — algebra