5.1. Definíció. Legyen  ⋅ egy komplexus és M egy modulus.
Alkalmazzuk a ⊗M funktort a
⋅ egy komplexus és M egy modulus.
Alkalmazzuk a ⊗M funktort a  ⋅ komplexusra, így kapjuk a
⋅ komplexusra, így kapjuk a  ⋅⊗M
komplexust:
⋅⊗M
komplexust:
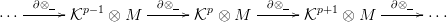
 ⋅ komplexust is, ami persze kanonikusan
izomorf
⋅ komplexust is, ami persze kanonikusan
izomorf  ⋅⊗ M-mel.
⋅⊗ M-mel.
5.1. Definíció. Legyen  ⋅ egy komplexus és M egy modulus.
Alkalmazzuk a ⊗M funktort a
⋅ egy komplexus és M egy modulus.
Alkalmazzuk a ⊗M funktort a  ⋅ komplexusra, így kapjuk a
⋅ komplexusra, így kapjuk a  ⋅⊗M
komplexust:
⋅⊗M
komplexust:
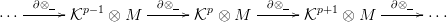
 ⋅ komplexust is, ami persze kanonikusan
izomorf
⋅ komplexust is, ami persze kanonikusan
izomorf  ⋅⊗ M-mel.
⋅⊗ M-mel.
5.2. Definíció. Legyenek  ⋅ és
⋅ és  ⋅ komplexusok. Az egyszerűség
kedvéért most ∂-val jelöljük a
⋅ komplexusok. Az egyszerűség
kedvéért most ∂-val jelöljük a  ⋅-beli differenciált, d-vel a
⋅-beli differenciált, d-vel a  ⋅
differenciálját. A tenzor szorzat komplexusuk az alábbi,
⋅
differenciálját. A tenzor szorzat komplexusuk az alábbi,  ⋅ ⊗
⋅ ⊗ ⋅-lel
jelölt kettős komplexus, melynben szintén ∂ és d betűk jelölik a két
differenciált:
⋅-lel
jelölt kettős komplexus, melynben szintén ∂ és d betűk jelölik a két
differenciált:
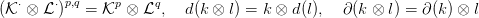
 ⋅⊗
⋅⊗ ⋅⋅ jelöli. (Más könyvekben
gyakran
⋅⋅ jelöli. (Más könyvekben
gyakran  ⋅⊗
⋅⊗ ⋅ jelöli a totális komplexust is.)
⋅ jelöli a totális komplexust is.)
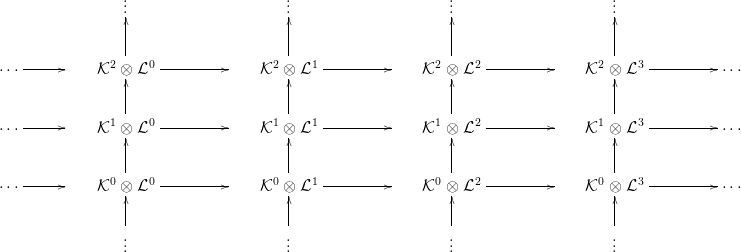 3. ábra. Tenzor szorzat komplexus
3. ábra. Tenzor szorzat komplexus
5.3. Feladat. Legyenek  ⋅ és
⋅ és  ⋅ komplexusok, tegyük fel, hogy
az egyik pontrahúzható (2.17. Következmény). Bizonyítsd be, hogy a
⋅ komplexusok, tegyük fel, hogy
az egyik pontrahúzható (2.17. Következmény). Bizonyítsd be, hogy a
 ⋅⊗
⋅⊗ ⋅ tenzor szorzat is pontrahúzható!
⋅ tenzor szorzat is pontrahúzható!
Ötlet: A tenzor szorzás funktor. Ezért ha egy homotópiát az identitással tenzor-szorzunk, homotópiát kapunk. □
5.4. Definíció. Legyenek M és N modulusok. Válasszunk egy
 ⋅ → M lapos feloldást (4.2. Definíció), most alsó indexet használunk
(1.2. Konvenció). Készítsük el az
⋅ → M lapos feloldást (4.2. Definíció), most alsó indexet használunk
(1.2. Konvenció). Készítsük el az  ⋅⊗N komplexust (5.1. Definíció).
Ennek az n-edik homológiája (alsó indexekkel, lásd az 1.2. Konvenciót)
a Tor n(M,N) modulus:
⋅⊗N komplexust (5.1. Definíció).
Ennek az n-edik homológiája (alsó indexekkel, lásd az 1.2. Konvenciót)
a Tor n(M,N) modulus:
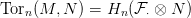
5.5. Megjegyzés. Bár a jelölésből most kimaradt, a tenzor szorzat, és így a Tor n modulusok is függenek az R gyűrűtől. Ha szükséges kiírnunk, akkor a pontosabb M ⊗RN illetve Tor NR(M,N) jelölések használhatók.
5.6. Megjegyzés. Most egy kommutatív gyűrű felett dolgozunk, ezért M ⊗ N és Tor n(M,N) is modulusok. Általában, ha S nem-kommutatív gyűrű, MS és SN jobb- illetve baloldali S-modulusok, akkor értelmezhetők az MS⊗SSN és a Tor nS(M S,SN) Abel csoportok, de ezek nem lesznek S-modulusok.
5.7. Lemma. Legyenek M és N modulusok. A Tor n(M,N) modulus
definíciója nem függ a feloldás választásától. Sőt, a másik tényező
tetszőleges 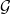 ⋅ → N lapos feloldásával kaphatunk egy alternatív
definíciót is:
⋅ → N lapos feloldásával kaphatunk egy alternatív
definíciót is:
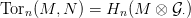
Ötlet:
Mind a két feloldást használjuk. Alkalmazzuk a 3.24. Következményt
az  ⋅⊗ N és az M ⊗
⋅⊗ N és az M ⊗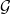 ⋅ komplexusokra, a kettős komplexus hiányzó
részét a
⋅ komplexusokra, a kettős komplexus hiányzó
részét a  ⋅⊗
⋅⊗ ⋅ tenzor szorzat komplexussal (5.2. Definíció) töltjük
ki.
⋅ tenzor szorzat komplexussal (5.2. Definíció) töltjük
ki.
Ezzel beláttuk, hogy az M feloldásából számított Tor n(M,N) modulus izomorf az N feloldásából számítottal, és ez utóbbi izomorf azzal, amit az M egy másik feloldásából kapunk. □
5.8. Feladat. Dolgozd ki részletesen az 5.7. Lemma bizonyítását!
5.9. Feladat. A tenzor-szorzat szimmetrikus. Lásd be, hogy a Tor n funktor is az:
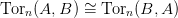
5.10. Tétel. Legyen 0 → A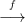 B
B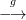 C → 0 egy rövid egzakt sorozat
és M egy modulus. Ekkor létezik az alábbi hosszú egzakt sorozat, amelyik
funktoriálisan függ a rövid egzakt sorozattól és M-től:
C → 0 egy rövid egzakt sorozat
és M egy modulus. Ekkor létezik az alábbi hosszú egzakt sorozat, amelyik
funktoriálisan függ a rövid egzakt sorozattól és M-től:
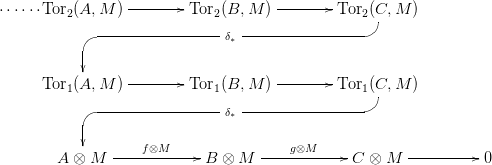
Bizonyítás. Alkalmazzuk a ⊗M funktort a 4.6. Lemmában készült szabad feloldásokra. Így komplexusok rövid egzakt sorozatához jutunk. Erre alkalmazzuk a 2.6. Tételt, így jutunk a kívánt egzakt sorozathoz. □
5.11. Feladat. Bizonyítsd be, hogy egy M modulus pontosan akkor lapos, ha Tor 1(M,N) = 0 minden N modulusra! Mutasd meg, hogy ilyenkor Tor n(M,N) = 0 minden n ≥ 1 egészre!
5.13. Feladat. Legyen R egy nullosztómentes főideálgyűrű.