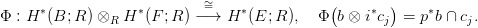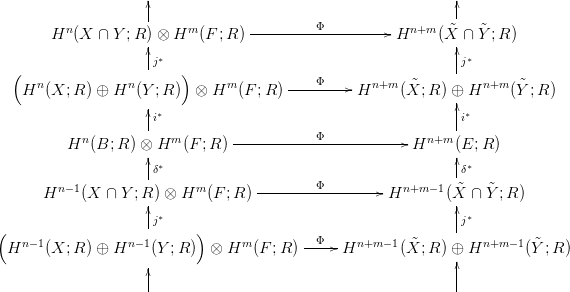Direkt szorzatok kohomológia-gyűrűjéről a Künneth tételek adnak nagyon
sok információt (lásd a 25. és a 26. szakaszokat). A direkt szorzat egyik
általánosítása a nyaláb fogalma (lásd a 12.2. Definíciót). Belátjuk, hogy
bizonyos feltételek mellett a nyalábok kohomológia-csoportjai is könnyen
számolhatók. A gyűrű-struktúráról viszont ez a módszer nem ad
számot.
28.1. Tétel (Leray-Hirsch). Legyen F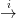 E
E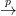 B egy nyaláb (12.2. Definíciót),
és R egy kommutatív gyűrű! A p∗ kohomológia-homomorfizmus segítségével
a H∗(E; R) kohomológia-gyűrű egy H∗(B; R)-modulusnak tekinthető (lásd a
27.10. Következmény (b) pontját). Tegyük fel, hogy
B egy nyaláb (12.2. Definíciót),
és R egy kommutatív gyűrű! A p∗ kohomológia-homomorfizmus segítségével
a H∗(E; R) kohomológia-gyűrű egy H∗(B; R)-modulusnak tekinthető (lásd a
27.10. Következmény (b) pontját). Tegyük fel, hogy
-
(a)
- Hn(F; R) végesen generált szabad R-modulus minden n-re,
-
(b)
- vannak olyan cj ∈ Hkj(E; R) kohomológia osztályok, amelyeknek
tetszőleges F rostra való i∗c
j megszorításai együttvéve a H∗(F; R)
szabad R-modulus bázisát alkotják.
Ekkor H∗(E; R) egy szabad H∗(B; R)-modulus, a c
j osztályok egy bázist
alkotnak. Az izomorfizmust megadjuk a csésze-szorzat segítségével:
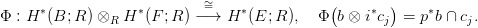
Bizonyítás. Most csak azzal az esettel foglalkozunk, amikor B
egy véges-dimenziós CW-komplexus, az általános eset könnyen
visszavezethető erre. Ha dim(B) = 0, akkor E felbomlik a rostjainak
diszjunkt uniójára, tehát H∗(E; R)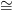 ∏
b∈BH∗(F; R), és a tétel igaz
ebben az esetben.
∏
b∈BH∗(F; R), és a tétel igaz
ebben az esetben.
Legyen most dim(B) = n > 0, a tételt n szerinti indukcióval
bizonyítjuk. Válasszunk minden n-cella belsejében egy tömör golyót,
legyen X ⊂ B a golyók uniója, és legyen Y ⊂ B az X halmaz
komplementumának lezártja. Legyen továbbá 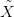 = p−1(X) és Ỹ =
p−1(Y ).
= p−1(X) és Ỹ =
p−1(Y ).
Látható, hogy X∩Y a golyók peremének uniója, azaz (n−1)-dimenziós,
Y pedig homotóp ekvivalens a B komplexus (n − 1)-vázával, tehát
szintén (n−1)-dimenziós. Mivel a golyók pontrahúzhatók, X homotóp
ekvivalens egy 0-dimenziós CW-komplexussal. Az indukciós feltétel
miatt tehát a tétel állítása igaz az F → 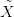 → X, az F → Ỹ → Y
és az F → (
→ X, az F → Ỹ → Y
és az F → (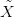 ∩Ỹ) → (X ∩ Y ) nyalábokra. Az alábbi diagrammon
a bal oldali oszlop a B = X ∪ Y felbontáshoz, a jobboldali pedig az
E =
∩Ỹ) → (X ∩ Y ) nyalábokra. Az alábbi diagrammon
a bal oldali oszlop a B = X ∪ Y felbontáshoz, a jobboldali pedig az
E =  ∪Ỹ felbontáshoz tartozó Mayer-Vietoris sorozatból származik:
∪Ỹ felbontáshoz tartozó Mayer-Vietoris sorozatból származik:
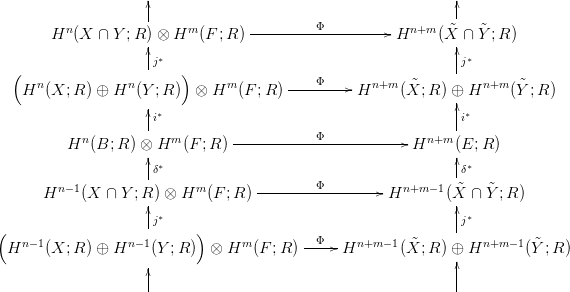
Az
i∗,
j∗,
δ∗ jelöléseket a
21.5. Tételből vettük át. A csésze-szorzat
funktorialitása miatt az
i∗-ot és a
j∗-ot tartalmazó téglalapok kommutatívak.
A
δ∗-ot tartalmazó téglalapok pedig a
8.6. Tétel miatt kommutatívak
(lásd még a
27.6. Tételt is). Az indukciós feltevés miatt a diagrammon
látható öt
Φ-vel jelölt homomorfizmus közül négy (a felső kettő és
az alsó kettő) izomorfizmus. Az 5-lemma (lásd a
2.9. Lemmát) miatt
tehát a középső
Φ is izomorfizmus.
□
Ötlet. Legyenek (F,F0) és (B,B0) tér-párok, és p : (E,E0) → B egy
(F,F0)-nyaláb (lásd a 12.3. Definíciót). Érdemes három változatot is
kimondani: az (E,E0), az  E,p−1(B
0)
E,p−1(B
0) , illetve az
, illetve az  E,E0 ∪ p−1(B
0)
E,E0 ∪ p−1(B
0) tér-párok kohomológiáira! □
tér-párok kohomológiáira! □
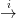 E
E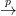 B egy nyaláb (12.2. Definíciót),
és R egy kommutatív gyűrű! A p∗ kohomológia-homomorfizmus segítségével
a H∗(E; R) kohomológia-gyűrű egy H∗(B; R)-modulusnak tekinthető (lásd a
27.10. Következmény (b) pontját). Tegyük fel, hogy
B egy nyaláb (12.2. Definíciót),
és R egy kommutatív gyűrű! A p∗ kohomológia-homomorfizmus segítségével
a H∗(E; R) kohomológia-gyűrű egy H∗(B; R)-modulusnak tekinthető (lásd a
27.10. Következmény (b) pontját). Tegyük fel, hogy