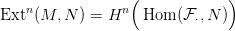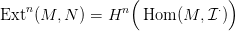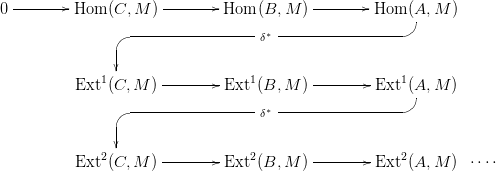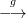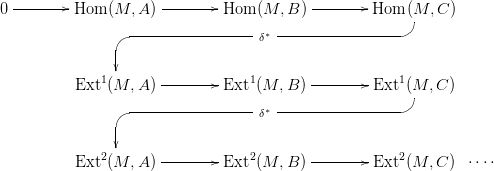6. Homomorfizmus komplexus, Ext funktor
6.1. Definíció. Legyen most M egy modulus,  ⋅ egy fölül-indexelt
komplexus,
⋅ egy fölül-indexelt
komplexus,  ⋅ pedig a következő alul-indexelt komplexus:
⋅ pedig a következő alul-indexelt komplexus:
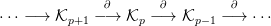 Ha a Hom( ,M) funktort a
Ha a Hom( ,M) funktort a  ⋅ komplexusra alkalmazzuk, akkor a
„sorrend megfordul”, az alábbi Hom(
⋅ komplexusra alkalmazzuk, akkor a
„sorrend megfordul”, az alábbi Hom( ⋅,M)⋅ (felül indexelt) komplexust
kapjuk:
⋅,M)⋅ (felül indexelt) komplexust
kapjuk:
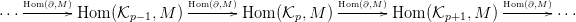 Ha pedig a Hom(M, ) funktort alkalmazzuk a
Ha pedig a Hom(M, ) funktort alkalmazzuk a  ⋅ komplexusra, akkor
„megmarad az eredeti sorrend”, az alábbi Hom(M,
⋅ komplexusra, akkor
„megmarad az eredeti sorrend”, az alábbi Hom(M, ⋅)⋅ (felül indexelt)
komplexust kapjuk:
⋅)⋅ (felül indexelt)
komplexust kapjuk:
6.2. Megjegyzés. Ha a Hom( ,M) funktort egy fölül indexelt
komplexusra alkalmazzuk, vagy ha a Hom(M, ) funktort egy alul
indexelt komplexusra alkalmazzuk, akkor az eredmény egy alul indexelt
komplexus lesz.
Ötlet: A Hom egy funktor. Ezért ha egy homotópiát az identitással
Hom-ozunk, homotópiát kapunk. □
6.6. Megjegyzés. Bár a jelölésből most kimaradt, a Hom modulus,
és így az Ext n modulusok is függenek az R gyűrűtől. Ha szükséges
kiírnunk, akkor a pontosabb Hom R(M,N) illetve Ext Rn(M,N)
jelölések használhatók.
6.7. Megjegyzés. Most egy kommutatív gyűrű felett dolgozunk,
ezért Hom(M,N) és Ext n(M,N) is modulusok. Általában, ha S
nem-kommutatív gyűrű, SM és SN mindketten baloldali S-modulusok,
akkor értelmezhetők az Hom S(SM,SN) és az Ext Sn(
SM,SN) Abel
csoportok, de ezek nem lesznek S-modulusok.
6.8. Lemma. Legyenek M és N modulusok. Az Ext n(M,N) modulus
definíciója nem függ a feloldás választásától. Sőt, a másik tényező
tetszőleges N → ⋅ injektív feloldásával (4.3. Definíció) kaphatunk egy
alternatív definíciót is:
⋅ injektív feloldásával (4.3. Definíció) kaphatunk egy
alternatív definíciót is:
6.9. Feladat. Bizonyítsd be a 6.8. Lemmát: imitáld az 5.7. Lemma
bizonyítát!
6.10. Feladat. Adnak-e a szokásos Hom-⊗ azonosságok Ext-Tor
azonosságokat?
Bizonyítás. Alkalmazzuk a Hom( ,M) funktort a 4.6. Lemmában
készült szabad feloldásokra. Így komplexusok rövid egzakt sorozatához
jutunk, Erre alkalmazzuk a 2.6. Tételt, így jutunk a kívánt egzakt
sorozathoz. □
Bizonyítás. Alkalmazzuk a Hom(M, ) funktort a 4.6. Lemmában
készült injektív feloldásokra. Így komplexusok rövid egzakt
sorozatához jutunk, Erre alkalmazzuk a 2.6. Tételt, így jutunk a
kívánt egzakt sorozathoz. □
Íme az 5.11. Feladat analógiája projektív és injektív modulusokkal:
6.13. Feladat. Bizonyítsd be, hogy egy M modulus pontosan akkor
projektív, ha Ext 1(M,N) = 0 minden N modulusra! Mutasd meg, hogy
ilyenkor Ext n(M,N) = 0 minden n ≥ 1 egészre!
6.14. Feladat. Bizonyítsd be, hogy egy M modulus pontosan akkor
injektív, ha Ext 1(N,M) = 0 minden N modulusra! Mutasd meg, hogy
ilyenkor Ext n(N,M) = 0 minden n ≥ 1 egészre!
 ⋅ egy fölül-indexelt
komplexus,
⋅ egy fölül-indexelt
komplexus,  ⋅ pedig a következő alul-indexelt komplexus:
⋅ pedig a következő alul-indexelt komplexus:
 ⋅ komplexusra alkalmazzuk, akkor a
„sorrend megfordul”, az alábbi Hom(
⋅ komplexusra alkalmazzuk, akkor a
„sorrend megfordul”, az alábbi Hom( ⋅,M)⋅ (felül indexelt) komplexust
kapjuk:
⋅,M)⋅ (felül indexelt) komplexust
kapjuk:
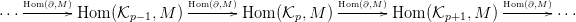
 ⋅ komplexusra, akkor
„megmarad az eredeti sorrend”, az alábbi Hom(M,
⋅ komplexusra, akkor
„megmarad az eredeti sorrend”, az alábbi Hom(M, ⋅)⋅ (felül indexelt)
komplexust kapjuk:
⋅)⋅ (felül indexelt)
komplexust kapjuk:
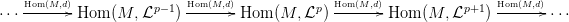
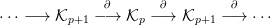

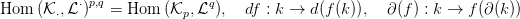

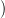

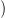
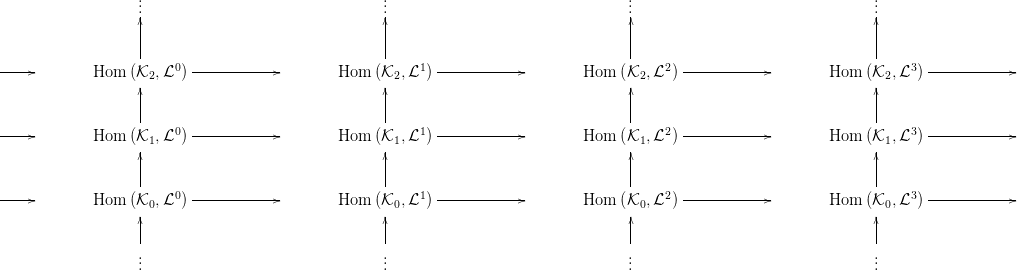 4. ábra. Homomorfizmus komplexus. Itt
4. ábra. Homomorfizmus komplexus. Itt