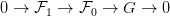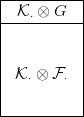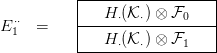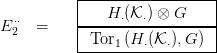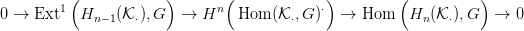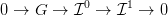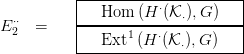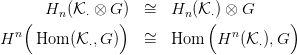7. Univerzális Együttható Tételek — algebra
Bizonyítás. Választunk egy kétlépéses szabad feloldást (lásd a
4.4. Tények (i) pontját):
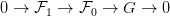
Ha ezt tenzor-szorozzuk a
 ⋅
⋅ komplexussal (lásd az
5.2. Definíciót)
az alábbi kettőskomplexushoz jutunk.
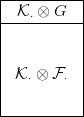
A
3.22. Következmény szerint a
 ⋅⊗ G
⋅⊗ G komplexus lánc-ekvivalens a
 ⋅ ⊗
⋅ ⊗ ⋅
⋅ szorzat totális komplexusával. A
 ⋅ ⊗
⋅ ⊗ ⋅
⋅ szorzat pedig egy
kétsoros kettős komplexus, alkalmazható rá a
3.26. Tétel. Mivel az
 n
n
modulusok szabadok, a velük való szorzás felcserélhető a homológia
funktorral (mert egzakt, lásd a
4.1. Definíciót). A
3.25. Definícióbeli
első táblázat így néz ki:
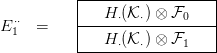
Ebből látható, hogy a második táblázat így alakul:
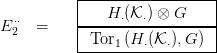
(lásd a
3.25. Definíciót és az
5.4. Definíciót). Tehát a
3.26. Tételben
szereplő egzakt sorozat megegyezik a bizonyítandó egzakt sorozattal,
és a
3.28. Tétel miatt felhasad.
□
7.2. Feladat. A 7.1. Tétel bizonyításában alsó indexeket használtunk
(1.2. Konvenció) míg a 3.26. Tételben felső indexek
vannak. Ellenőrizd, hogy helyesen alkalmaztuk a 3.26. Tételt! Mutasd
meg, hogy a kapott egzakt sorozat valóban funktoriálisan függ  ⋅-tól és
G-től!
⋅-tól és
G-től!
7.3. Feladat. A
7.1. Tétel bizonyításában használtuk a 3.22. Következményt. Lásd be,
hogy a szóbanforgó kettős komplexus oszlopai valóban egzaktak!
Bizonyítás. Választunk egy kétlépéses injektív feloldást (lásd a
4.4. Tények (i) pontját):
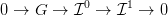
Alkalmazzuk a
Hom funktort a
 ⋅
⋅ komplexusra és erre a feloldásra
(lásd a
6.3. Definíciót), az alábbi kettőskomplexushoz jutunk:
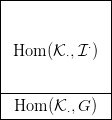
A
3.22. Következmény szerint a
Hom( ⋅,G)
⋅,G) komplexus lánc-ekvivalens
a
Hom( ⋅,
⋅,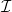 ⋅)
⋅) totális komplexusával. A
Hom( ⋅,
⋅,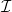 ⋅)
⋅) pedig egy kétsoros
kettős komplexus, alkalmazható rá a
3.26. Tétel. Mivel az
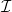 n
n modulus
injektív, a
Hom( ,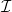 n)
n) funktor felcserélhető a homológia funktorral
(mert egzakt, lásd a
4.1. Definíciót). A
3.25. Definícióbeli első táblázat
így néz ki:

Ebből látható, hogy a második táblázat így alakul:
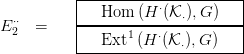
(lásd a
3.25. Definíciót és az
5.4. Definíciót). Tehát a
3.26. Tétel
egzakt sorozata megegyezik a bizonyítandó egzakt sorozattal, és a
3.28. Tétel miatt felhasad.
□
7.5. Feladat. Ellenőrizd a 7.4. Tétel bizonyításában az indexeket!
Mutasd meg, hogy a kapott egzakt sorozat valóban funktoriálisan függ
 ⋅-tól és G-től!
⋅-tól és G-től!
7.6. Feladat. A
7.4. Tétel bizonyításában használtuk a 3.22. Következményt. Lásd be,
hogy a szóbanforgó kettős komplexus oszlopai valóban egzaktak!
7.7. Feladat. A 7.1. Tételben a Tor 1 csoport a jobboldalon áll,
míg a 7.4. Tételben az Ext 1 csoport a baloldalon bukkan fel.
Hogyan lehetséges ez — hiszen mindkét tételt a 3.22. Következmény
segítségével bizonyítottuk?
7.8. Feladat. Adott egy F test. Legyen  ⋅ egy F-vektortér komplexus és
F ≤ G egy testbővítés. Lásd be, hogy
⋅ egy F-vektortér komplexus és
F ≤ G egy testbővítés. Lásd be, hogy
 ⋅ egy szabad modulusokból
épült komplexus (alul indexelt, lásd az 1.2. Konvenciót) és G egy
tetszőleges modulus. Minden n-re létezik egy egzakt sorozat:
⋅ egy szabad modulusokból
épült komplexus (alul indexelt, lásd az 1.2. Konvenciót) és G egy
tetszőleges modulus. Minden n-re létezik egy egzakt sorozat:
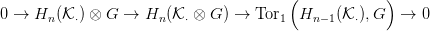
 ⋅-tól és G-től. Az egzakt sorozat felhasad.
(A felhasadás nem kanonikus.)
⋅-tól és G-től. Az egzakt sorozat felhasad.
(A felhasadás nem kanonikus.)