8.1. Tétel. Legyenek  ⋅ és
⋅ és  ⋅ modulus komplexusok! Ekkor minden
p,q párra létezik egy természetes külső szorzás (angolul cross product):
⋅ modulus komplexusok! Ekkor minden
p,q párra létezik egy természetes külső szorzás (angolul cross product):
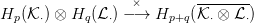
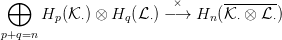
8.1. Tétel. Legyenek  ⋅ és
⋅ és  ⋅ modulus komplexusok! Ekkor minden
p,q párra létezik egy természetes külső szorzás (angolul cross product):
⋅ modulus komplexusok! Ekkor minden
p,q párra létezik egy természetes külső szorzás (angolul cross product):
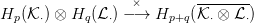
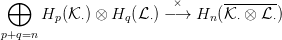
Bizonyítás. Jelölje ∂, d illetve D a három komplexus ( ⋅,
⋅,  ⋅ és a
szorzat) differenciálját! Tekintsük az alábbi részkomplexusokat:
⋅ és a
szorzat) differenciálját! Tekintsük az alábbi részkomplexusokat:
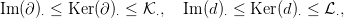
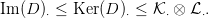
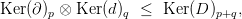
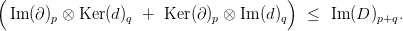
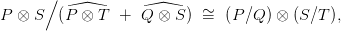 | (1) |
ahol  és
és  a részmodulusok tenzorszorzatának képét jelöli a
P ⊗ S tenzorszorzatban. □
a részmodulusok tenzorszorzatának képét jelöli a
P ⊗ S tenzorszorzatban. □
8.2. Feladat. Igazold az (1) azonosságot!
8.3. Tétel. Legyen 0 →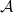 ⋅ →
⋅ →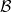 ⋅ →
⋅ →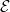 ⋅ → 0 komplexusok egy rövid
egzakt sorozata,
⋅ → 0 komplexusok egy rövid
egzakt sorozata,  ⋅ egy modulus komplexus. Tegyük fel, hogy
⋅ egy modulus komplexus. Tegyük fel, hogy 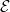 ⋅ lapos
modulusokból áll, így még két egzakt sorozathoz jutunk:
⋅ lapos
modulusokból áll, így még két egzakt sorozathoz jutunk:
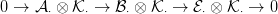
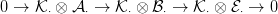

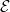 ⋅
⋅ és k ∈
Hq(
és k ∈
Hq( ⋅) homológia-osztályokre teljesülnek a következő külső szorzat
azonosságok:
⋅) homológia-osztályokre teljesülnek a következő külső szorzat
azonosságok:
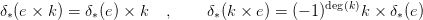
Bizonyítás. Jelölje d, ∂ és D a 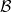 ⋅,
⋅,  ⋅ és
⋅ és 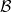 ⋅⊗
⋅⊗ ⋅ komplexusok
differenciálját! Válasszunk az e, k elemekhez e ∈
⋅ komplexusok
differenciálját! Válasszunk az e, k elemekhez e ∈ 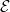 p és k ∈
p és k ∈  q
reprezentánsokat! Az alábbi kommutatív diagramon a függőleges
nyilak a k-val való külső szorzást reprezentálják:
q
reprezentánsokat! Az alábbi kommutatív diagramon a függőleges
nyilak a k-val való külső szorzást reprezentálják:
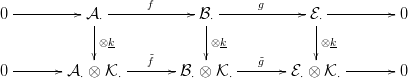
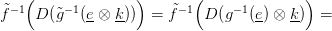
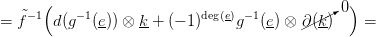
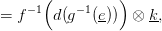
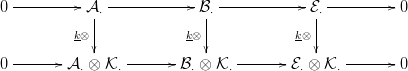
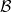 ⋅⊗
⋅⊗ ⋅ szorzat differenciálját. Most
is ∂(k) = 0, tehát a 2.6. Tétel szerint a δ∗(k × e) homológia-osztályt
az alábbi lánc reprezentálja:
⋅ szorzat differenciálját. Most
is ∂(k) = 0, tehát a 2.6. Tétel szerint a δ∗(k × e) homológia-osztályt
az alábbi lánc reprezentálja:
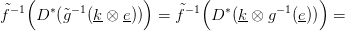
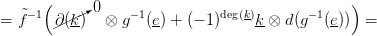
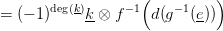
8.4. Feladat. A 8.1. Tétel segítségével építs ilyen külső szorzatot is:
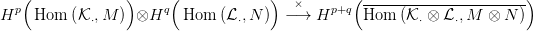
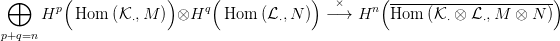
Ötlet: Lineáris függvények szorzata bi-lineáris, ez ad egy (modulusokra vonatkozó) funktoriális homomorfizmust:
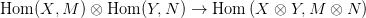
8.5. Feladat. Az előzőek mintájára építs ilyen külső szorzatot is (alsó, és felső indexekkel):
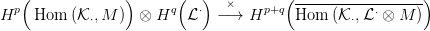
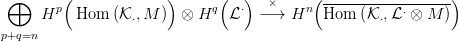
8.6. Tétel. Legyen 0 → ⋅ →
⋅ →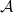 ⋅ →
⋅ →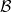 ⋅ → 0 komplexusok egy rövid
egzakt sorozata,
⋅ → 0 komplexusok egy rövid
egzakt sorozata,  ⋅ egy modulus komplexus. Legyenek továbbá M és N
tetszőleges modulusok. Tegyük fel, hogy
⋅ egy modulus komplexus. Legyenek továbbá M és N
tetszőleges modulusok. Tegyük fel, hogy  ⋅ és
⋅ és  ⋅ projektív modulusokból
áll, így még három egzakt sorozathoz jutunk:
⋅ projektív modulusokból
áll, így még három egzakt sorozathoz jutunk:
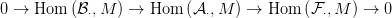
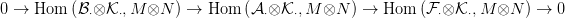
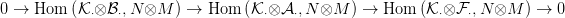
 Hom(
Hom( ⋅,M)
⋅,M) és k ∈
Hq
és k ∈
Hq Hom(
Hom( ⋅,N)
⋅,N) homológia-osztályokre teljesülnek a következő külső
szorzat azonosságok:
homológia-osztályokre teljesülnek a következő külső
szorzat azonosságok:
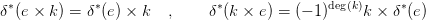
Ötlet: Imitáld a 8.3. Tétel bizonyítását! □
8.7. Feladat. Miért nem következik a 8.6. Tétel a 8.3. Tételből? Keress olyan általánosítást, amelyikből már következik!