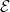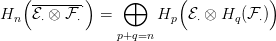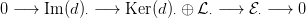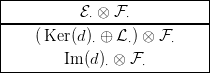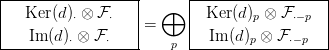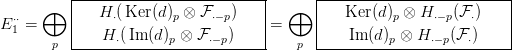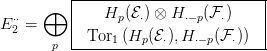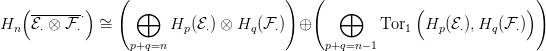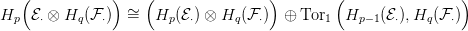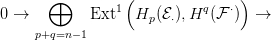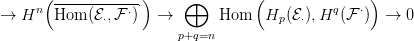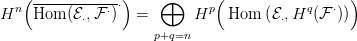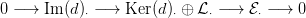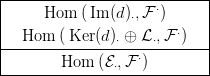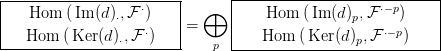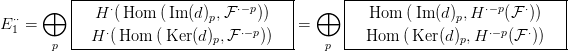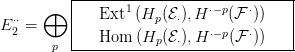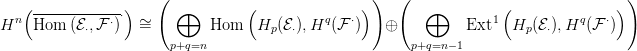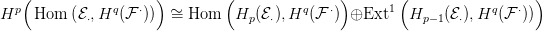10. Általános Künneth tételek — algebra
Az előző fejezetben olyan szituációkat kerestünk, amikor pontosan ki tudjuk
számolni bizonyos komplexusok tenzor szorzatának a homológiáit. Most
ennél sokkal általánosabb tenzor szorzatok homológiáit vizsgáljuk. Az
általánosságnak ára van: pontos formulák helyett csak egzakt sorozatokat
kapunk.
Bizonyítás. Mivel d2 = 0, azért Im(d)⋅ ≤ Ker(d)⋅. A 4.4. Tények
(h) pontja miatt Im(d)⋅ és Ker(d)⋅ szabad modulusokból áll, és
a definícióból azonnal következik, hogy a differenciáljuk (tehát
d megszorítása) nulla. Tekintsük a d : 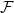 ⋅ → Im(d)⋅+1
lánc-homomorfizmust. Elkészítjük hozzá a 3.10. Definícióbeli egzakt
sorozatot. Állítjuk, hogy ez kielégíti a lemma követelményeit.
⋅ → Im(d)⋅+1
lánc-homomorfizmust. Elkészítjük hozzá a 3.10. Definícióbeli egzakt
sorozatot. Állítjuk, hogy ez kielégíti a lemma követelményeit.
Valóban, a sorozatban szereplő leképezés-kúp szemmel látjatóan
szabad Abel csoportokból épült, és a 3.18. Feladat miatt homotóp
ekvivalens Ker(d)⋅-vel. Ezért a homológiái is szabad modulusok, a
9.3. Lemma megadja a keresett direkt összeg felbontást. □
Bizonyítás. Jelölje d az 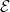 ⋅ komplexus differenciálját. A 10.1. Lemma
ad egy
⋅ komplexus differenciálját. A 10.1. Lemma
ad egy
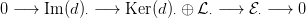
egzakt sorozatot. Alkalmazzuk rá a
⊗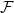 ⋅
⋅ funktort, így kajuk az
alábbi háromsoros diagramot:
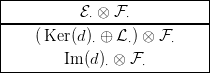
Úgy indexelünk, hogy az elválasztó vonal alatt van a nulladik sor,
fölötte pedig az első. Ez valójában egy „hármas komplexus”, de most
kettős komplexusként kezeljük: a sorokba a megfelelő totális komplexust
írjuk. A
3.22. Következmény szerint a felső sor lánc-ekvivalens az
alsó két sor totális komplexusával. Erre a kétsoros kettős komplexusra
alkalmazzuk a
3.26. Tételt. Be fogjuk látni, hogy a kapott egzakt
sorozat megegyezik az általunk keresett sorozattal. A felhasadás tehát
a
3.28. Tételből következik.
Mivel 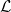 ⋅ pontrahúzható, azért az
⋅ pontrahúzható, azért az 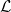 ⋅⊗
⋅⊗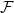 ⋅ szorzat is az (5.3. Feladat).
Az E1⋅⋅ táblázatban a sorok homológiáját kell írni, tehát a
⋅ szorzat is az (5.3. Feladat).
Az E1⋅⋅ táblázatban a sorok homológiáját kell írni, tehát a 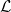 ⋅⊗
⋅⊗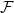 ⋅ tagot
bátran elhagyhatjuk az első sorból. A megmaradó kettős komplexusban
a vízszintes irányú differenciálok nullák (10.1. Lemma: Im(d)⋅ és
Ker(d)⋅ differenciálja nulla), tehát az alábbi direkt összegre bomlik:
⋅ tagot
bátran elhagyhatjuk az első sorból. A megmaradó kettős komplexusban
a vízszintes irányú differenciálok nullák (10.1. Lemma: Im(d)⋅ és
Ker(d)⋅ differenciálja nulla), tehát az alábbi direkt összegre bomlik:
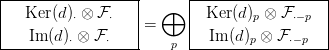
A
Ker(d)p és az
Im(d)p szorzók szabad modulusok, a velük való szorzás
egzakt funktor, tehát az
E1⋅⋅ táblázat így alakul:
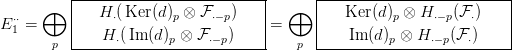
Másrészt a
0 → Im(d)p → Ker(d)p → Hp(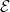 ⋅) → 0
⋅) → 0 egzakt sorozat
éppen a
Hp( ⋅)
⋅) szabad feloldása. Az ebben szereplő
Im(d)p → Ker(d)p
homomorfizmust
Hq( p)
p)-vel szorozva éppen az
E1⋅⋅ táblázat
p-edik
összeadandójának egy oszlopát kapjuk. Éppen ez a komplexus szerepel
a
Tor funktor definíciójában (
5.4. Definíció), tehát az
E2⋅⋅ táblázat
így alakul:
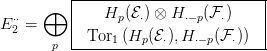
A
3.26. Tételből tehát valóban a keresett egzakt sorozatot kapjuk,
és az valóban felhasad. Ebből következik az alábbi (nem kanonikus)
izomorfizmus:
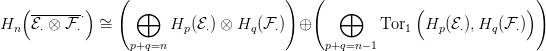
Számítsuk ki a
Hp
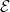 ⋅⊗Hq(
⋅⊗Hq(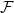 ⋅)
⋅)
csoportot az Univerzális Együttható
tétel (
7.1. Tétel) segítségével:
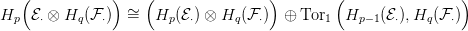
Ezt összegezve az olyan
p,q párokra, amelyek összege
n, éppen a fenti
izomorfizmus jobb oldalát kapjuk. Ez bizonyítja a
10.2. Tétel utolsó
egyenletét.
□
10.3. Feladat. A 10.2. Tétel bizonyításában alsó
indexekkel dolgoztunk, míg a felhasznált korábbi lemmákban, tételekben
felső indexek szerepelnek. Ellenőrizd, hogy helyesen alkalmaztuk-e őket
(azaz jól hoztuk-e alulra az indexeket)!
Bizonyítás. Jelölje d az 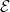 ⋅ komplexus differenciálját. A 10.1. Lemma
ad egy
⋅ komplexus differenciálját. A 10.1. Lemma
ad egy
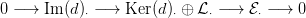
egzakt sorozatot. Alkalmazzuk rá a
Hom( , ⋅)
⋅) funktort (ez megfordítja
a sorrendet, és fölül-indexelt komplexust ad, lásd a
6.3. Definíció), így
kapjuk az alábbi háromsoros diagramot:
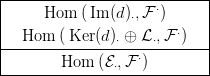
Most úgy indexelünk, hogy az elválasztó vonal fölött van a nulladik
sor, alatta pedig a
(−1)-edik! Ez valójában egy „hármas komplexus”,
de most kettős komplexusként kezeljük: a sorokba a megfelelő totális
komplexust írjuk. A
3.22. Következmény szerint az alsó sor lánc-ekvivalens
az fölső két sor totális komplexusával. Erre a kétsoros kettős komplexusra
alkalmazzuk a
3.26. Tételt. Be fogjuk látni, hogy a kapott egzakt
sorozat megegyezik az általunk keresett sorozattal. A felhasadás tehát
a
3.28. Tételből következik.
Mivel  ⋅ pontrahúzható, azért a Hom
⋅ pontrahúzható, azért a Hom 
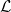 ⋅,
⋅,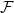 ⋅
⋅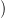 komplexus is az
(6.4. Feladat). Az E1⋅⋅ táblázatban a sorok homológiáját kell írni,
tehát a Hom
komplexus is az
(6.4. Feladat). Az E1⋅⋅ táblázatban a sorok homológiáját kell írni,
tehát a Hom 
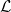 ⋅,
⋅,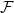 ⋅
⋅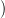 tagot bátran elhagyhatjuk az első sorból. A
megmaradó kettős komplexusban a vízszintes irányú differenciálok
nullák (10.1. Lemma: Im(d)⋅ és Ker(d)⋅ differenciálja nulla), tehát az
alábbi direkt összegre bomlik:
tagot bátran elhagyhatjuk az első sorból. A
megmaradó kettős komplexusban a vízszintes irányú differenciálok
nullák (10.1. Lemma: Im(d)⋅ és Ker(d)⋅ differenciálja nulla), tehát az
alábbi direkt összegre bomlik:
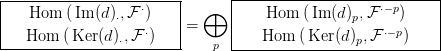
Most
Ker(d)p és
Im(d)p szabad modulusok, a velük való
Hom-ozás
egzakt funktor, tehát az
E1⋅⋅ táblázat így alakul:
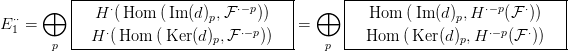
Másrészt a
0 → Im(d)p → Ker(d)p → Hp(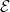 ⋅) → 0
⋅) → 0 egzakt sorozat
éppen a
Hp(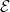 ⋅)
⋅) szabad feloldása. Az ebben szereplő
Im(d)p → Ker(d)p
homomorfizmusra alkalmazzuk a
Hom  ,Hq(
,Hq(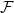 p)
p)
funktort — így
éppen az
E1⋅⋅ táblázat
p-edik összeadandójának egy oszlopát kapjuk.
Éppen ez a komplexus szerepel az
Ext funktor definíciójában (
6.5. Definíció),
tehát az
E2⋅⋅ táblázat így alakul:
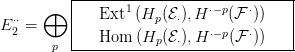
A
3.26. Tételből tehát valóban a keresett egzakt sorozatot kapjuk,
és az valóban felhasad. Ebből következik az alábbi (nem funktoriális)
izomorfizmus:
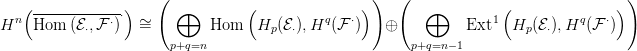
Számítsuk ki a
Hp Hom
Hom 
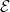 ⋅,Hq(
⋅,Hq(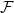 ⋅)
⋅)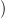

csoportot az Univerzális Együttható
tétel (
7.1. Tétel) segítségével:
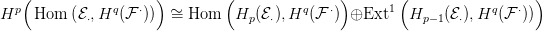
Ezt összegezve az olyan
p,q párokra, amelyek összege
n, éppen a fenti
izomorfizmus jobb oldalát kapjuk. Ez bizonyítja a
10.4. Tétel utolsó
egyenletét.
□
10.5. Feladat. A 10.4. Tétel bizonyításában részben alsó indexekkel
is dolgoztunk, míg a felhasznált korábbi lemmákban, tételekben felső
indexek szerepelnek. Ellenőrizd, hogy helyesen alkalmaztuk-e őket (azaz
jól hoztuk-e alulra az indexeket)!
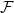 ⋅ egy szabad Abel csoportokból épült
komplexus, d jelölia differenciálját. Tekintsük az Im(d)⋅ ≤ Ker(d)⋅ ≤
⋅ egy szabad Abel csoportokból épült
komplexus, d jelölia differenciálját. Tekintsük az Im(d)⋅ ≤ Ker(d)⋅ ≤
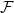 ⋅ rész-komplexusokat: ezek szabad Abelcsoportokból állnak, és a
differenciáljuk nulla. Konstruálható egy
⋅ rész-komplexusokat: ezek szabad Abelcsoportokból állnak, és a
differenciáljuk nulla. Konstruálható egy
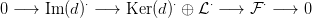
 ⋅ egy (szabad Abel csoportokból álló) pontrahúzható
komplexus.
⋅ egy (szabad Abel csoportokból álló) pontrahúzható
komplexus.