Univerzalis Egyutthato Tetelek

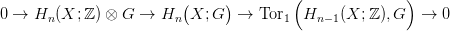
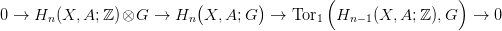
Az univerzális együttható tételekre úgy érdemes gondolni, hogy az egészegyütthatós homológia-csoportok „lényegében meghatározzák” a tetszőleges G együtthatóval számolt homológia- és kohomológia-csoportokat.

23.1. Tétel (Univerzális Együttható tétel homológiára). Legyen X egy topológikus tér, G egy együttható csoport. Minden n-re létezik egy egzakt sorozat, amelyik funktoriálisan függ X-től és G-től:

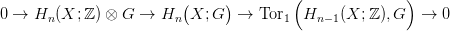
( ) ( ) 0 → Hn (X; ℤ) ⊗ G → Hn X; G → Tor1 Hn −1(X; ℤ),G → 0

Legyen most (X,A) egy tér-pár (11.1. Definíció). Ehhez is tartozik egy egzakt sorozat, amelyik funktoriálisan függ az (X,A) pártól és G-től:

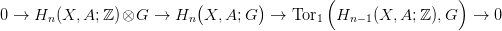
( ) 0 → H (X, A; ℤ )⊗G → H (X, A;G ) → Tor H (X, A;ℤ ),G → 0 n n 1 n−1

A fenti egzakt sorozatok felhasadnak. (A felhasadás nem kanonikus.)

23.2. Tétel (Univerzális Együttható tétel kohomológiára). Legyen X egy topológikus tér, G egy együttható csoport. Minden n-re létezik egy egzakt sorozat:

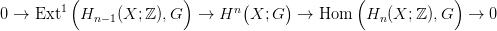
( ) ( ) ( ) 0 → Ext1 Hn −1(X; ℤ ),G → Hn X; G → Hom Hn (X; ℤ),G → 0

amelyik funktoriálisan függ X-től és G-től. Legyen most (X,A) egy topológikus pár (11.1. Definíció). Ehhez is tartozik egy egzakt sorozat:

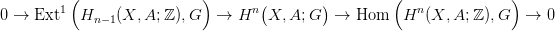
1( ) n( ) ( n ) 0 → Ext Hn −1(X, A;ℤ ),G → H X,A; G → Hom H (X, A;ℤ ),G → 0

amelyik funktoriálisan függ az (X,A) pártól és G-től. A fenti egzakt sorozatok felhasadnak. (A felhasadás nem kanonikus.)

Az univerzális együttható tételek egy variációja pedig azt mutatja, hogy (bizonyos végességi feeltételek mellett) az egészegyütthatós kohomológia-csoportok is „lényegében meghatározzák” a tetszőleges G együtthatóval számolt homológia- és kohomológia-csoportokat.

23.3. Tétel (Univerzális Együttható tétel komológiára II.). Legyen X egy topológikus tér, G egy együttható csoport. Tegyük fel vagy azt, hogy G végesen generált, vagy pedig azt, hogy Hⁿ(X; ℤ) végesen generált minden n-re. Ekkor minden n-re létezik egy egzakt sorozat:

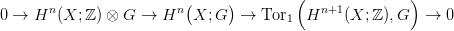
( ) ( ) 0 → Hn (X; ℤ) ⊗ G → Hn X; G → Tor1 Hn+1 (X; ℤ ),G → 0

amelyik funktoriálisan függ X-től és G-től. Legyen most (X,A) egy topológikus pár (11.1. Definíció) most is feltesszük vagy azt, hogy G végesen generált, vagy pedig azt, hogy Hⁿ(X,A; ℤ) végesen generált minden n-re. Ekkor minden n-re létezik egy egzakt sorozat:

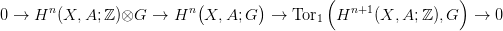
( ) ( ) 0 → Hn (X, A;ℤ )⊗G → Hn X, A;G → Tor1 Hn+1 (X, A; ℤ),G → 0

amelyik funktoriálisan függ az (X,A) pártól és G-től. Ezek az egzakt sorozatok felhasadnak. (A felhasadás nem kanonikus.)

Bizonyítás. Alkalmazzuk a 7.1. Tételt a Hom Δ⋅(X), ℤ illetve a Hom Δ⋅(X,A), ℤ komplexusokra. Menet közben használni kell az alábbi azonosságot:

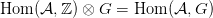Hom (A, ℤ) ⊗ G = Hom (A, G )

(7)

ahol 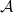is egy Abel csoport, és vagy 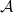vagy G végesen generált. □

23.4. Feladat. Lásd be a (7) azonosságot (az ott megadott feltételek mellett)! Mutass rá ellenpéldát abban az esetben, ha sem 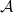sem G nem végesen generált!

23.5. Feladat. A 23.3. Tétel Tor ₁-es tagjában és az alábbi 23.6. Tétel Ext ¹-es tagjában (n + 1)-edik kohomológia szerepel, pedig a bizonyításban használt 7.1. Tételben és a 7.4. Tételben (n − 1)-edik homológia szerepelt. Hogyan lehetséges ez?

23.6. Tétel (Univerzális Együttható tétel homológiára II.). Legyen X egy topológikus tér, G egy együttható csoport. Tegyük fel, hogy Hⁿ(X; ℤ) végesen generált minden n-re. Ekkor minden n-re létezik egy egzakt sorozat, amelyik funktoriálisan függ X-től és G-től:

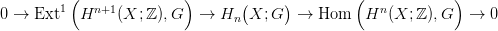
( ) ( ) ( ) 0 → Ext1 Hn+1 (X; ℤ ),G → Hn X; G → Hom Hn (X; ℤ ),G → 0

Legyen most (X,A) egy topológikus pár (11.1. Definíció) Ehhez is tartozik egy egzakt sorozat, amelyik funktoriálisan függ az (X,A) pártól és G-től:

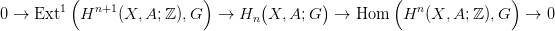
1( n+1 ) ( ) ( n ) 0 → Ext H (X, A;ℤ ),G → Hn X,A; G → Hom H (X, A;ℤ ),G → 0

A fenti egzakt sorozatok felhasadnak. (A felhasadás nem kanonikus.)

Bizonyítás. A 4.9. Lemma segítségével választunk végesen generált szabad approximációkat a Hom Δ⋅(X), ℤés a Hom Δ⋅(X,A), ℤ Abel csoport komplexusokhoz. Ezekre alkalmazzuk a 7.4. Tételt. Menet közben használni kell az alábbi azonosságot:

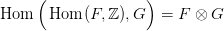( ) Hom Hom (F, ℤ),G = F ⊗ G

(8)

ahol F egy végesen generált szabad Abel csoport. □

23.7. Feladat. Lásd be a (8) azonosságot (az ott megadott feltételek mellett)! Mutass rá ellenpéldát abban az esetben, ha F nem szabad, vagy nem végesen generált!

23. Univerzális Együttható Tételek — topológia