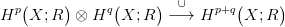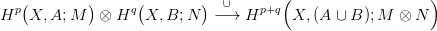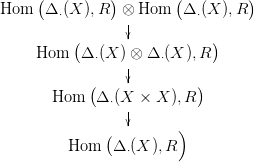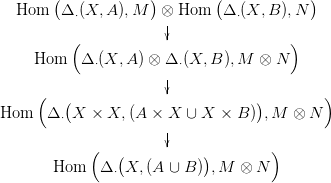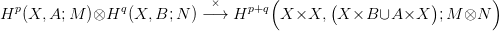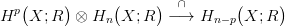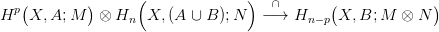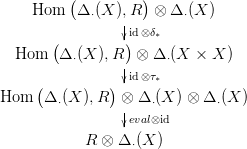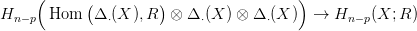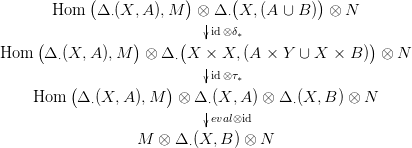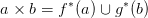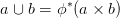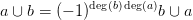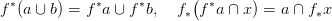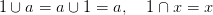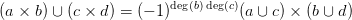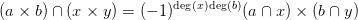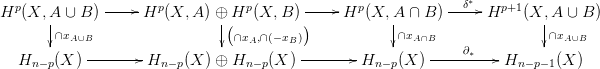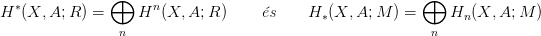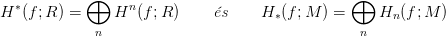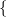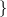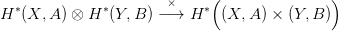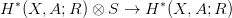27. Szorzat struktúrák
27.2. Feladat. A 24.1. Konstrukció ad egy
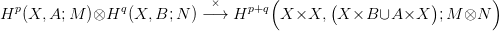 homomorfizmust, ezt komponáljuk az X → X×X átló menti visszahúzással.
Lásd be, hogy éppen a 27.1. Konstrukcióbeli csésze szorzást kapjuk!
homomorfizmust, ezt komponáljuk az X → X×X átló menti visszahúzással.
Lásd be, hogy éppen a 27.1. Konstrukcióbeli csésze szorzást kapjuk!
27.3. Konstrukció (sapka szorzat). Legyen X egy topológikus tér,
A,B ≤ X alterek, M és N modulusok egy R gyűrű fölött. Tegyük
fel, hogy {A,B} jól vág (21.2. Definíció). Megépítjük az alábbi sapka
szorzás homomorfizmusokat (angolul: cap product):
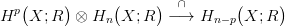
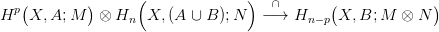 Mindkét sorozat minden változóban természetes transzformáció.
Mindkét sorozat minden változóban természetes transzformáció.
Az alábbi diagrammon az első lánc-homomorfizmus az X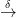 X × X
átlós leképezésből, a második az Eilenberg-Zilber tétel
(22.2. Következmény) τ∗ lánc-ekvivalenciájából származik, a harmadik
leképezés pedig a Hom
X × X
átlós leképezésből, a második az Eilenberg-Zilber tétel
(22.2. Következmény) τ∗ lánc-ekvivalenciájából származik, a harmadik
leképezés pedig a Hom  Δ⋅(X),R
Δ⋅(X),R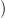 -beli homomorfizmusok kiértékelése
az első Δ⋅(X) elemein, tehát egy f ⊗ x ⊗ y alakú szorzathoz az f(x)y
elemet rendeli:
-beli homomorfizmusok kiértékelése
az első Δ⋅(X) elemein, tehát egy f ⊗ x ⊗ y alakú szorzathoz az f(x)y
elemet rendeli:
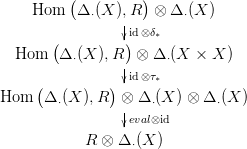 Fontos észrevétel, hogy amíg az első két leképezés lánc-homomorfizmus,
a harmadik, eval ⊗ id, csak fokszámtartó abelcsoport homomorfizmus,
de nem feltétlenül kommutál a komplexusok határ-homomorfizmusával.
Ezzel szemben ha c egy tetszőleges kolánc Hom
Fontos észrevétel, hogy amíg az első két leképezés lánc-homomorfizmus,
a harmadik, eval ⊗ id, csak fokszámtartó abelcsoport homomorfizmus,
de nem feltétlenül kommutál a komplexusok határ-homomorfizmusával.
Ezzel szemben ha c egy tetszőleges kolánc Hom  Δ⋅(X),R
Δ⋅(X),R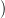 -ben, azaz
∂c = 0, akkor a {c}⊗ Δ⋅(X) ⊗ Δ⋅(X)
-ben, azaz
∂c = 0, akkor a {c}⊗ Δ⋅(X) ⊗ Δ⋅(X)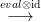 R ⊗ Δ⋅(X) leképezés egy
lánc-homomorfizmus.
R ⊗ Δ⋅(X) leképezés egy
lánc-homomorfizmus.
A tenzor-szorzat totális komplexusában most alsó indexeket fogunk
használni. Az egyik tényező felső indexet használ — szokásunkhoz híven
ezt negatívan számítjuk a totális komplexus indexébe. Tehát a 8.1. Tétel
és a diagrammon szereplő első két lánc-homomorfizmus segítségével
kapunk egy
 homomorfizmust. Könnyű ellenőrizni, hogy eval ⊗ id is indukál egy
homomorfizmust. Könnyű ellenőrizni, hogy eval ⊗ id is indukál egy
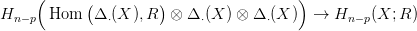 homomorfizmust, annak ellenére, hogy ő maga nem lánc-homomorfizmus.
Az utóbbi két homomorfizmus kompozíciója a sapka szorzás. A térpárokra
vonatkozó sapka szorzást pedig az alábbi diagrammból kapjuk:
homomorfizmust, annak ellenére, hogy ő maga nem lánc-homomorfizmus.
Az utóbbi két homomorfizmus kompozíciója a sapka szorzás. A térpárokra
vonatkozó sapka szorzást pedig az alábbi diagrammból kapjuk:
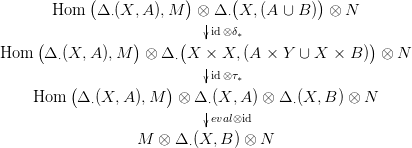
27.4. Feladat. Lást be, hogy a
27.3. Konstrukcióban szereplő eval ⊗ id leképezés, annak ellenére, hogy
nem lánc-homomorfizmus, mégiscsak indukál egy leképezést a megfelelő
homológia csopotok között!
27.5. Tétel. Legyenek (X,A) és (Y,B) tér-párok, és tegyük fel, hogy
{X × B,A × Y } jól vág (21.2. Definíció). Lelölje f : X × Y → X és
g : X × Y → Y a vetítéseket. Ekkor tetszőleges a ∈ Hp(X,A; M) és
b ∈ Hq(X,B; N) kohomológia-osztályokra:
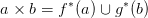 Másrészt, ha X = Y , akor a feltétel miatt {A,B} jól vág, és a ϕ :
X → X × X átlós leképezés (ϕ(x) = (x,x)) segítségével:
Másrészt, ha X = Y , akor a feltétel miatt {A,B} jól vág, és a ϕ :
X → X × X átlós leképezés (ϕ(x) = (x,x)) segítségével:
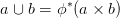
27.6. Tétel (Szorzat-azonosságok). Rögzítsünk egy R gyűrűt. Az
alábbi azonosságokban minden homológiát és kohomológiát R-modulus
együtthatókkal számolunk. a,b,c,d kohomológia-osztályokat, x,y pedig
homológia-osztályokat jelölnek, 1 jelöli
a konstans 1 kohomológia-osztályt (17.4. Definíció, olyan esetben, ha
az együttható-csoport éppen R), f terek vagy tér-párok közti folytonos
függvény. Nem részletezzük, hogy pontosan melyik térhez vagy térpárhoz
tartoznak — az azonosságok minden olyan esetben érvényesek, ha a
bennük előírt műveletek elvégezhetők:
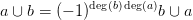

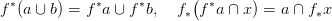
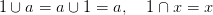
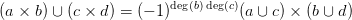
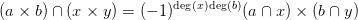
Ötlet: Minden következik a korábbi eredményekből:
8.6. Tétel, 22.6. Feladat, 22.7. Következmény, 22.9. Konstrukció,
27.5. Tétel. □
Most megvizsgáljuk, mi a kapcsolat a különféle szorzások, és a Mayer-Vietoris
sorozatokban (21.5. Tétel) szereplő ∂∗ illetve δ∗ homomorfizmusok között.
A Mayer-Vietoris sorozat egy rövid egzakt komplexus-sorozathoz tartozó
hosszú egzakt sorozat, tehát a 8.3. Tételtől és a 8.6. Tételtől várhatjuk,
hogy a kívánt azonosságokat adják.
27.7. Tétel (Sapka-szorzás és a Mayer-Vietoris sorozat). Legyenek
A,B alterek egy X topológikus térben. Tegyük fel, hogy {A,B} jól vág.
Legyen xA∩B ∈ Hn X,A ∩ B; ℤ
X,A ∩ B; ℤ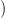 egy tetszőleges homológia osztály,
jelölje xA, xB és xA∪B az xA∩B képét a Hn(X,A), Hn(X,B) illetve
Hn(X,A ∪ B) homológia-csoportokban. Az alábbi két sora az (X,A) ∪
(X,B) =
egy tetszőleges homológia osztály,
jelölje xA, xB és xA∪B az xA∩B képét a Hn(X,A), Hn(X,B) illetve
Hn(X,A ∪ B) homológia-csoportokban. Az alábbi két sora az (X,A) ∪
(X,B) =  X,A ∪ B
X,A ∪ B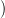 fedéshez, illetve az X ∪ X = X fedéshez tartozó
Mayer-Vietoris sorozatok részlete (lásd a 21.5. Tételt), a diagramm
előjel erejéig kommutatív:
fedéshez, illetve az X ∪ X = X fedéshez tartozó
Mayer-Vietoris sorozatok részlete (lásd a 21.5. Tételt), a diagramm
előjel erejéig kommutatív:
27.8. Feladat. Keresd meg a 27.7. Tétel egy csésze-szorzásra
vonatkozó változatát!
27.9. Definíció. Legyen (X,A) egy tér-pár, M modulus az R gyűrű
felett. Bevezetjük a
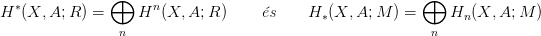 jelöléseket. Az elsőt
jelöléseket. Az elsőt kohomológia-gyűrűnek
, a másikat pedig homológia-modulusnak
hívjuk. Ha f egy térpárok közti leképezés, akkor
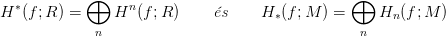 jelöli a hozzá tartozó homomorfizmusokat. Ha A = ∅, akkor kihagyható
a jelölésből: H∗(X; R), H
∗(X; M). Ha egyértelmű, hogy melyik gyűrűről
illetve modulusról van szó, akkor az együttható is elhagyható: H∗(X,A),
H∗(X), H∗(f) illetve H
∗(X,A), H∗(X), H∗(f).
jelöli a hozzá tartozó homomorfizmusokat. Ha A = ∅, akkor kihagyható
a jelölésből: H∗(X; R), H
∗(X; M). Ha egyértelmű, hogy melyik gyűrűről
illetve modulusról van szó, akkor az együttható is elhagyható: H∗(X,A),
H∗(X), H∗(f) illetve H
∗(X,A), H∗(X), H∗(f).
A 27.6. Tétel azonosságaiból azonnal látható:
27.10. Következmény. Rögzítsük az R gyűrűt és az M modulust!
Minden kohomológia R együtthatóval, minden homológia M együtthatóval
értendő. A tenzor szorzásokat R felett végezzük.
-
(a)
- Minden
(X,A) tér-párra H∗(X,A) a csésze szorzással egy fokszámozott,
ferdén kommutatív R-algebra, H∗(X,A) a sapka-szorzással egy
fokszámozott H∗(X,A)-modulus.
-
(b)
- Minden f : (X,A) → (Y,B) pár-leképezésre H∗(f)
egy fokszámozott R-algebra homomorfizmus. Ez fokszámozott
H∗(Y,B)-modulussá teszi az (X,A) pár homológiáját is, és H
∗(f)
egy H∗(Y,B)-modulus homomorfizmus.
-
(c)
- Legyenek (X,A) és (Y,B) tér-párok, tegyük fel, hogy
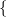 A ×
Y,X×B
A ×
Y,X×B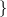 jól vág (21.2. Definíció). Tekintsük az (X,A)×(Y,B)
szorzat-párt (11.1. Definíció). R-algebrák tenzor szorzata ismét
R-algebra, a kohomológia külső szorzás (24.1. Konstrukció) egy
fokszámozott algebra-homomorfizmus:
jól vág (21.2. Definíció). Tekintsük az (X,A)×(Y,B)
szorzat-párt (11.1. Definíció). R-algebrák tenzor szorzata ismét
R-algebra, a kohomológia külső szorzás (24.1. Konstrukció) egy
fokszámozott algebra-homomorfizmus:
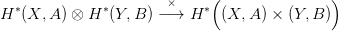 Ez fokszámozott H∗(X,A)⊗H∗(Y,B)-modulussá teszi a szorzat-pár
homológiáját is, a homológia külső szorzás (24.2. Feladat) egy
H∗(X,A) ⊗ H∗(Y,B)-modulus homomorfizmus:
Ez fokszámozott H∗(X,A)⊗H∗(Y,B)-modulussá teszi a szorzat-pár
homológiáját is, a homológia külső szorzás (24.2. Feladat) egy
H∗(X,A) ⊗ H∗(Y,B)-modulus homomorfizmus:

-
(d)
- Legyen most S egy R-algebra, és N egy S-modulus, és ϕ :
M ⊗ S → N egy S-modulus homomorfizmus. Ez indukál egy
S-algebra homomorfizmust:
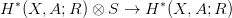 és egy H∗(X,A; R) ⊗ S-modulus homomorfizmust:
és egy H∗(X,A; R) ⊗ S-modulus homomorfizmust: